Lý thuyết Các số đặc trưng đo mức độ phân tán của mẫu số liệu - SGK Toán 10 CTST

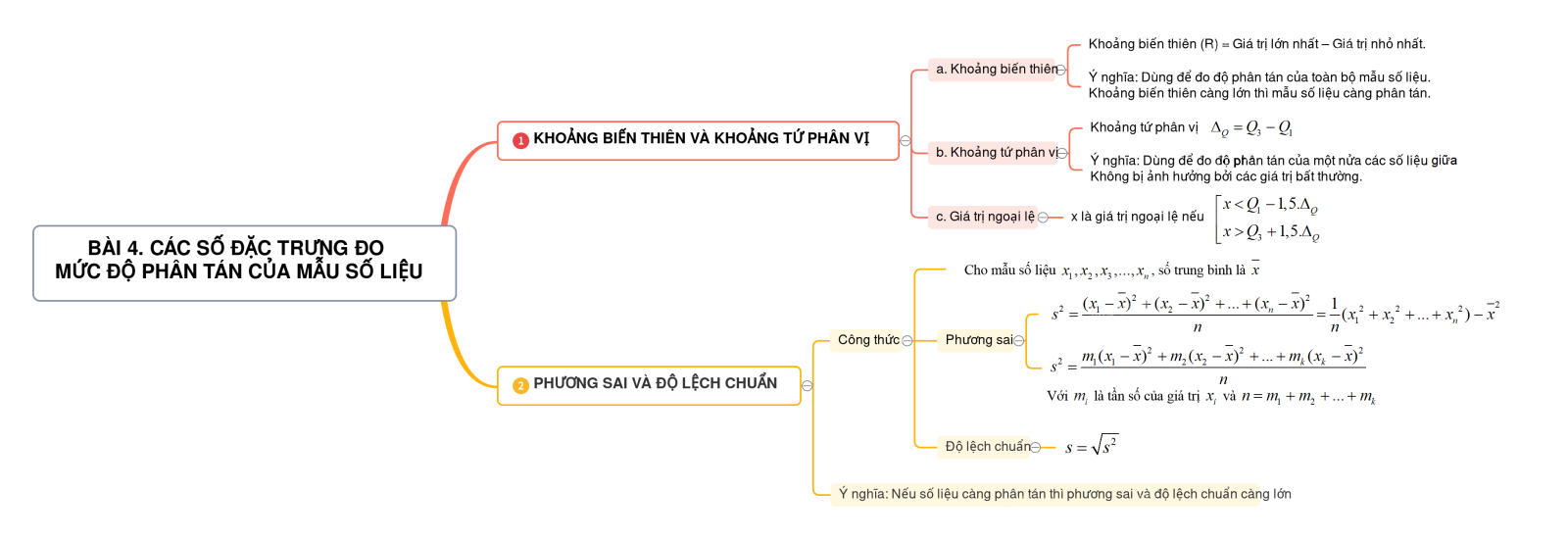
1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ
a. Khoảng biến thiên
Khoảng biến thiên (R) = Giá trị lớn nhất – Giá trị nhỏ nhất.
Ý nghĩa: Dùng để đo độ phân tán của toàn bộ mẫu số liệu: Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
b. Khoảng tứ phân vị
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
Ý nghĩa: Dùng để đo độ phân tán của một nửa các số liệu có giá trị thuộc đoạn từ \({Q_1}\) đến \({Q_3}\) trong mẫu.
Không bị ảnh hưởng bởi các giá trị bất thường.
c. Giá trị ngoại lệ
\(x\) là giá trị ngoại lệ nếu \(\left[ \begin{array}{l}x < {Q_1} - 1,5.{\Delta _Q}\\x > {Q_3} + 1,5.{\Delta _Q}\end{array} \right.\)
2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN
Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\), số trung bình là \(\overline x \)
+ Phương sai: \({s^2} = \frac{{{{({x_1} - \overline x )}^2} + {{({x_2} - \overline x )}^2} + ... + {{({x_n} - \overline x )}^2}}}{n} = \frac{1}{n}({x_1}^2 + {x_2}^2 + ... + {x_n}^2) - {\overline x ^2}\)
+ Độ lệch chuẩn: \(s = \sqrt {{s^2}} \)
Ý nghĩa: Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn
Chú ý: Phương sai của mẫu số liệu cho dạng bảng tần số:
\({s^2} = \frac{{{m_1}{{({x_1} - \overline x )}^2} + {m_2}{{({x_2} - \overline x )}^2} + ... + {m_k}{{({x_k} - \overline x )}^2}}}{n}\)
Với \({m_i}\) là tần số của giá trị \({x_i}\) và \(n = {m_1} + {m_2} + ... + {m_k}\)