Lý thuyết các định nghĩa

Câu hỏi: 1. Định nghĩa 
- Vectơ là một đoạn thẳng có hướng.
- Vectơ có điểm đầu là \(A\), điểm cuối \(B\) kí hiệu \(\overrightarrow{AB}\) và đọc là "vectơ \(AB\)". Khi không cần chỉ rõ điểm đầu, điểm cuối vectơ còn được kí hiệu \(\overrightarrow{a}\), \(\overrightarrow{b}\)...

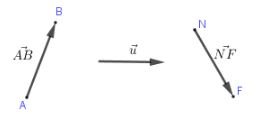
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.
2. Vec tơ cùng phương, vectơ cùng hướng.
- Hai vec tơ cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng.

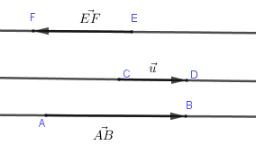
3. Hai vectơ bằng nhau
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó hay nói gọn hơn, độ dài của vectơ \(\overrightarrow{AB}\) là độ dài đoạn thẳng \(AB\), kí hiệu \(\left | \overrightarrow{AB} \right |\)
\(\left | \overrightarrow{AB} \right |  = AB\).
Độ dài vectơ là một số không âm.
Vec tơ có độ dài bằng \(1\) gọi là vectơ đơn vị.
- Hai vectơ bằng nhau nếu chúng cùng hướng  và có cùng độ dài.

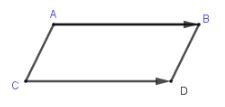
\(\overrightarrow{AB}\) = \(\overrightarrow{CD}\) \(\Leftrightarrow\)  \(\overrightarrow{AB}\) cùng hướng với \(\overrightarrow{CD}\) và \(\left | \overrightarrow{AB} \right |\) = \(\left | \overrightarrow{CD} \right |\)
- Khi cho trước một vectơ \(\overrightarrow{a}\) và một vectơ \(0\) trong mặt phẳng, ta luôn tìm được một điểm \(A\) để có \(\overrightarrow{OA}\) = \(\overrightarrow{a}\).
Điểm \(A\) như vậy là duy nhất.
4. Vec tơ- không
Vectơ- không kí hiệu là \(\overrightarrow{0}\) là vectơ có điểm đầu và điểm cuối trùng nhau:
\(\overrightarrow{AA}\) = \(\overrightarrow{BB}\) = \(\overrightarrow{0}\)
Vectơ- không có độ dài bằng \(0\) và hướng tùy ý.