Giúp em bài này
Kiến trúc sư thiết kế một con đường để chia khu đất hình chữ nhật $ABCD$ với $AB=40m,AD=60m$ thành hai phần (hai lề đường là các đường cong $HEK$ và $PQIR$ ). Trong đó phần giới hạn bởi đường cong $HEK$ và các đoạn $AH,AB,BK$ là sân chơi, phần giới hạn bởi đường cong $PQIR$ và các đoạn $PD,DC,CR$ để trồng hoa (tham khảo hình vẽ). Nếu gắn một hệ trục toạ độ vuông góc có trục hoành, trục tung lần lượt cùng phương với các đường thẳng $AB,AD$ thì đường cong $PQIR$ là một phần của đồ thị hàm số bậc ba $y=f(x)$ ;
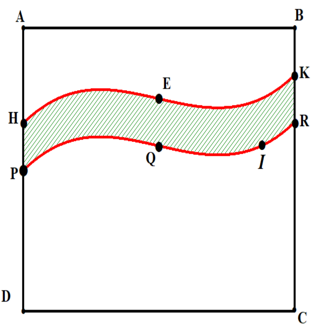
Đường cong $HEK$ nhận được bằng cách tịnh tiến đường cong $PQIR$ theo phương thẳng đứng lên phía trên $10m$.
Biết $AP=30m,BR=20m$, điểm $Q$ cách các cạnh $AB,AD$
lần lượt $25m$ và $20m$, điểm $I$ cách các cạnh $AB,AD$ lần lượt $25m$ và $35m$. Gọi ${{S}_{1}}$ là diện tích phần sân chơi và ${{S}_{2}}$ là diện tích phần trồng hoa. Tính $\dfrac{{{S}_{1}}}{{{S}_{2}}}$ (làm tròn kết quả đến hàng phần trăm).
Sưu tầm: Để thi sở GD tỉnh Hải Dương 2025
Kiến trúc sư thiết kế một con đường để chia khu đất hình chữ nhật $ABCD$ với $AB=40m,AD=60m$ thành hai phần (hai lề đường là các đường cong $HEK$ và $PQIR$ ). Trong đó phần giới hạn bởi đường cong $HEK$ và các đoạn $AH,AB,BK$ là sân chơi, phần giới hạn bởi đường cong $PQIR$ và các đoạn $PD,DC,CR$ để trồng hoa (tham khảo hình vẽ). Nếu gắn một hệ trục toạ độ vuông góc có trục hoành, trục tung lần lượt cùng phương với các đường thẳng $AB,AD$ thì đường cong $PQIR$ là một phần của đồ thị hàm số bậc ba $y=f(x)$ ;
Đường cong $HEK$ nhận được bằng cách tịnh tiến đường cong $PQIR$ theo phương thẳng đứng lên phía trên $10m$.
Biết $AP=30m,BR=20m$, điểm $Q$ cách các cạnh $AB,AD$
lần lượt $25m$ và $20m$, điểm $I$ cách các cạnh $AB,AD$ lần lượt $25m$ và $35m$. Gọi ${{S}_{1}}$ là diện tích phần sân chơi và ${{S}_{2}}$ là diện tích phần trồng hoa. Tính $\dfrac{{{S}_{1}}}{{{S}_{2}}}$ (làm tròn kết quả đến hàng phần trăm).
Sưu tầm: Để thi sở GD tỉnh Hải Dương 2025
Last edited: