Câu hỏi: Giải mục 1 trang 105, 106 SGK Toán 11 tập 1 - Kết nối tri thức
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,01?
Phương pháp giải:
Dựa vào công thức số hạng tổng quát tìm được 5 số hạng đầu tiên và biểu diễn trên trục số.
Lời giải chi tiết:
a) \({u_1} = - 1; {u_2} = \frac{1}{2}; {u_3} = - \frac{1}{3}; {u_4} = \frac{1}{4}; {u_5} = - \frac{1}{5}\).
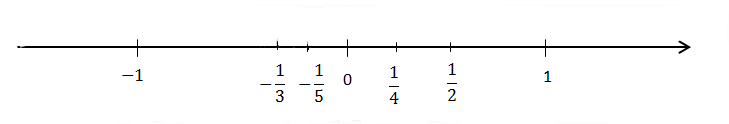
b) Ta có: \({u_{100}} = 0,01\) suy ra bắt đầu từ số hạng thứ 101 khoảng cách từ số hạng đến 0 nhỏ hơn 0,01.
Phương pháp giải:
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Lời giải chi tiết:
\(\left| {{u_n}} \right| = \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\) có thể nhỏ hơn một số dương bé tùy ý khi n đủ lớn.
Ta có: \(\left| {{u_n}} \right| < 1.69 \times {10^{ - 5}}\) ta cần n > 10.
Vậy các số hạng của dãy số kể từ số hạng thứ 11 đều có giá trị nhỏ hơn \(1.69 \times {10^{ - 5}}\).
Phương pháp giải:
Dãy sô \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực nếu \(\left( {{u_n} - a} \right) = 0\).
Lời giải chi tiết:
\({u_n} = {u_n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n}}}{n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n} - n}}{n} = \frac{{{{\left( { - 1} \right)}^n}}}{n} \to 0\) khi \(n \to + \infty \).
Do vậy \({v_n} = 0\).
Phương pháp giải:
\({u_n} = a\) khi và chỉ khi \(\left( {{u_n} - a} \right) = 0\).
Lời giải chi tiết:
\({u_n} = \frac{{3 \times {2^n} - 1}}{{{2^n}}} - 3 = \frac{{3 \times {2^n} - 1 - 3 \times {2^n}}}{{{2^n}}} = - \frac{1}{{{2^n}}} \to 0\) khi \(n \to + \infty \).
Do vậy \({u_n} = 3\).
Phương pháp giải:
\({u_n} = a\) khi và chỉ khi \(\left( {{u_n} - a} \right) = 0\).
Tìm được độ cao của quả bóng sau mỗi lần chạm sàn là cấp số nhân.
Lời giải chi tiết:
Độ cao của quả bóng sau mỗi lần chạm sàn tạo thành cấp số nhân có số hạng tổng quát:
\({u_n} = 5 \times {\left( {\frac{2}{3}} \right)^{n - 1}}\).
Ta có: \({\left( {\frac{2}{3}} \right)^{n - 1}} \to 0\) khi \(n \to + \infty \).
Suy ra \(5{\left( {\frac{2}{3}} \right)^{n - 1}} \to 0\) khi \(n \to + \infty \).
Vậy \({u_n} = 0\).
Hoạt động 1
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\)a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,01?
Phương pháp giải:
Dựa vào công thức số hạng tổng quát tìm được 5 số hạng đầu tiên và biểu diễn trên trục số.
Lời giải chi tiết:
a) \({u_1} = - 1; {u_2} = \frac{1}{2}; {u_3} = - \frac{1}{3}; {u_4} = \frac{1}{4}; {u_5} = - \frac{1}{5}\).
b) Ta có: \({u_{100}} = 0,01\) suy ra bắt đầu từ số hạng thứ 101 khoảng cách từ số hạng đến 0 nhỏ hơn 0,01.
Luyện tập 1
Chứng minh rằng: \(\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}} = 0\).Phương pháp giải:
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Lời giải chi tiết:
\(\left| {{u_n}} \right| = \frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{3^n}}}\) có thể nhỏ hơn một số dương bé tùy ý khi n đủ lớn.
Ta có: \(\left| {{u_n}} \right| < 1.69 \times {10^{ - 5}}\) ta cần n > 10.
Vậy các số hạng của dãy số kể từ số hạng thứ 11 đều có giá trị nhỏ hơn \(1.69 \times {10^{ - 5}}\).
Hoạt động 2
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). Xét dãy số \(\left( {{v_n}} \right)\) xác định bởi \({v_n} = {u_n} - 1\). Tính \({v_n} \).Phương pháp giải:
Dãy sô \(\left( {{u_n}} \right)\) có giới hạn là số thực a khi n dần tới dương vô cực nếu \(\left( {{u_n} - a} \right) = 0\).
Lời giải chi tiết:
\({u_n} = {u_n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n}}}{n} - 1 = \frac{{n + {{\left( { - 1} \right)}^n} - n}}{n} = \frac{{{{\left( { - 1} \right)}^n}}}{n} \to 0\) khi \(n \to + \infty \).
Do vậy \({v_n} = 0\).
Luyện tập 2
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{3.2}^n} - 1}}{{{2^n}}}\). Chứng minh rằng \(\mathop {lim}\limits_{n \to + \infty } {u_n} = 3\).Phương pháp giải:
\({u_n} = a\) khi và chỉ khi \(\left( {{u_n} - a} \right) = 0\).
Lời giải chi tiết:
\({u_n} = \frac{{3 \times {2^n} - 1}}{{{2^n}}} - 3 = \frac{{3 \times {2^n} - 1 - 3 \times {2^n}}}{{{2^n}}} = - \frac{1}{{{2^n}}} \to 0\) khi \(n \to + \infty \).
Do vậy \({u_n} = 3\).
Vận dụng 1
Một quả bóng cao su được thả từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng \(\frac{2}{3}\) độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử \({u_n}\) là độ cao (tính bằng mét) của quả bóng sau lần nảy lên thứ n. Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn là 0.Phương pháp giải:
\({u_n} = a\) khi và chỉ khi \(\left( {{u_n} - a} \right) = 0\).
Tìm được độ cao của quả bóng sau mỗi lần chạm sàn là cấp số nhân.
Lời giải chi tiết:
Độ cao của quả bóng sau mỗi lần chạm sàn tạo thành cấp số nhân có số hạng tổng quát:
\({u_n} = 5 \times {\left( {\frac{2}{3}} \right)^{n - 1}}\).
Ta có: \({\left( {\frac{2}{3}} \right)^{n - 1}} \to 0\) khi \(n \to + \infty \).
Suy ra \(5{\left( {\frac{2}{3}} \right)^{n - 1}} \to 0\) khi \(n \to + \infty \).
Vậy \({u_n} = 0\).