Câu hỏi: Cho \(A = \{ x \in \mathbb{R}|1 - 2x \le 0\} ,\)\(B = \{ x \in \mathbb{R}|x - 2 < 0\} .\)
Tìm \(A \cap B,A \cup B.\)
Tìm \(A \cap B,A \cup B.\)
Phương pháp giải
Liệt kê các phần tử của A và B.
\(A \cap B = \left\{ {x \in A| x \in B} \right\}\)
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\)
Lời giải chi tiết
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
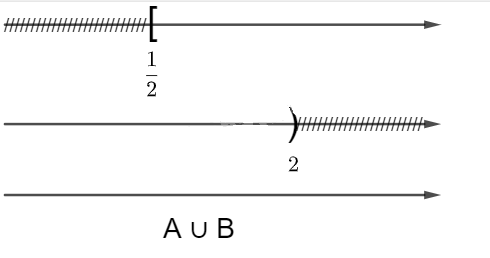
Vậy \(A \cup B = \mathbb R\)
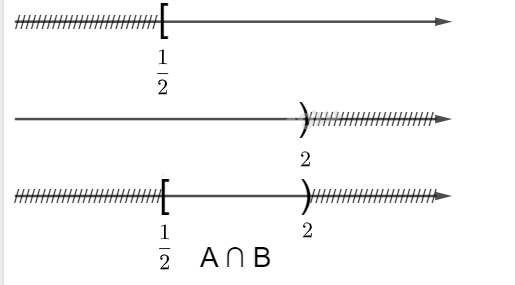
Vậy \(A \cap B = [\frac{1}{2};2)\)
Liệt kê các phần tử của A và B.
\(A \cap B = \left\{ {x \in A| x \in B} \right\}\)
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\)
Lời giải chi tiết
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
Vậy \(A \cup B = \mathbb R\)
Vậy \(A \cap B = [\frac{1}{2};2)\)