Câu hỏi: Cho tam giác ABC đều cạnh a. Các điểm M, N lần lượt thuộc các tia BC và CA thoả mãn \(BM = \frac{1}{3}BC,CN = \frac{5}{4}CA\). Tính:
a) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BN} \)
b) MN
a) \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {BN} \)
b) MN
Phương pháp giải
Bước 1: Sử dụng định nghĩa tích vô hướng của 2 vectơ để tính \(\overrightarrow {AB} .\overrightarrow {AC} \)
Bước 2: Biến đổi \(\overrightarrow {AM} ,\overrightarrow {BN} \) thành các vectơ chung gốc (gốc C) rồi tính \(\overrightarrow {AM} .\overrightarrow {BN} \)
Bước 3: Sử dụng các quy tắc và định nghĩa tích vô hướng của hai vectơ để tính \(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} } \right)^2}\) rồi tính độ dài MN
Lời giải chi tiết
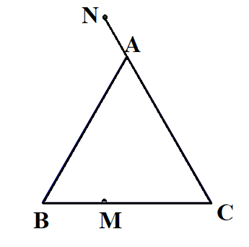
a) Ta có:
* \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)
* \(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\overrightarrow {CM} - \overrightarrow {CA} } \right)\left( {\overrightarrow {CN} - \overrightarrow {CB} } \right) = \overrightarrow {CM} .\overrightarrow {CN} - \overrightarrow {CM} .\overrightarrow {CB} - \overrightarrow {CA} .\overrightarrow {CN} + \overrightarrow {CA} .\overrightarrow {CB} \)
Ta có: + \(\overrightarrow {CM} .\overrightarrow {CN} = CM.CN.\cos \widehat {MCN} = \frac{{2a}}{3}.\frac{{5a}}{4}.\cos {60^0} = \frac{{5{a^2}}}{{12}}\)
+ \(\overrightarrow {CM} .\overrightarrow {CB} = \frac{2}{3}\overrightarrow {CB} .\overrightarrow {CB} = \frac{2}{3}B{C^2} = \frac{{2{a^2}}}{3}\)
+ \(\overrightarrow {CA} .\overrightarrow {CN} = \overrightarrow {CA} .\frac{5}{4}\overrightarrow {CA} = \frac{5}{4}A{C^2} = \frac{{5{a^2}}}{4}\)
+ \(\overrightarrow {CA} .\overrightarrow {CB} = CA.CB.\cos \widehat {ACB} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BN} = \overrightarrow {CM} .\overrightarrow {CN} - \overrightarrow {CM} .\overrightarrow {CB} - \overrightarrow {CA} .\overrightarrow {CN} + \overrightarrow {CA} .\overrightarrow {CB} = \frac{{5{a^2}}}{{12}} - \frac{{2{a^2}}}{3} - \frac{{5{a^2}}}{4} + \frac{{{a^2}}}{2} = - {a^2}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\), \(\overrightarrow {AM} .\overrightarrow {BN} = - {a^2}\)
b) Ta có: \(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} } \right)^2} = {\left( { - \frac{1}{3}\overrightarrow {BC} + \overrightarrow {BC} + \frac{5}{4}\overrightarrow {CA} } \right)^2}\)
\( = {\left( {\frac{2}{3}\overrightarrow {BC} + \frac{5}{4}\overrightarrow {CA} } \right)^2} = \frac{4}{9}B{C^2} + \frac{{25}}{{16}}A{C^2} + \frac{5}{3}\overrightarrow {BC} .\overrightarrow {CA} \)
\( = \frac{{289}}{{144}}{a^2} - \frac{5}{3}\overrightarrow {CB} .\overrightarrow {CA} = \frac{{289}}{{144}}{a^2} - \frac{5}{3}.CB.CA.\cos \widehat {BCA}\) \( = \frac{{289}}{{144}}{a^2} - \frac{5}{6}{a^2} = \frac{{169{a^2}}}{{144}}\)
\( \Rightarrow M{N^2} = \frac{{169{a^2}}}{{144}} \Rightarrow MN = \frac{{13a}}{{12}}\)
Bước 1: Sử dụng định nghĩa tích vô hướng của 2 vectơ để tính \(\overrightarrow {AB} .\overrightarrow {AC} \)
Bước 2: Biến đổi \(\overrightarrow {AM} ,\overrightarrow {BN} \) thành các vectơ chung gốc (gốc C) rồi tính \(\overrightarrow {AM} .\overrightarrow {BN} \)
Bước 3: Sử dụng các quy tắc và định nghĩa tích vô hướng của hai vectơ để tính \(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} } \right)^2}\) rồi tính độ dài MN
Lời giải chi tiết
a) Ta có:
* \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)
* \(\overrightarrow {AM} .\overrightarrow {BN} = \left( {\overrightarrow {CM} - \overrightarrow {CA} } \right)\left( {\overrightarrow {CN} - \overrightarrow {CB} } \right) = \overrightarrow {CM} .\overrightarrow {CN} - \overrightarrow {CM} .\overrightarrow {CB} - \overrightarrow {CA} .\overrightarrow {CN} + \overrightarrow {CA} .\overrightarrow {CB} \)
Ta có: + \(\overrightarrow {CM} .\overrightarrow {CN} = CM.CN.\cos \widehat {MCN} = \frac{{2a}}{3}.\frac{{5a}}{4}.\cos {60^0} = \frac{{5{a^2}}}{{12}}\)
+ \(\overrightarrow {CM} .\overrightarrow {CB} = \frac{2}{3}\overrightarrow {CB} .\overrightarrow {CB} = \frac{2}{3}B{C^2} = \frac{{2{a^2}}}{3}\)
+ \(\overrightarrow {CA} .\overrightarrow {CN} = \overrightarrow {CA} .\frac{5}{4}\overrightarrow {CA} = \frac{5}{4}A{C^2} = \frac{{5{a^2}}}{4}\)
+ \(\overrightarrow {CA} .\overrightarrow {CB} = CA.CB.\cos \widehat {ACB} = a.a.\cos {60^0} = \frac{{{a^2}}}{2}\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BN} = \overrightarrow {CM} .\overrightarrow {CN} - \overrightarrow {CM} .\overrightarrow {CB} - \overrightarrow {CA} .\overrightarrow {CN} + \overrightarrow {CA} .\overrightarrow {CB} = \frac{{5{a^2}}}{{12}} - \frac{{2{a^2}}}{3} - \frac{{5{a^2}}}{4} + \frac{{{a^2}}}{2} = - {a^2}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\), \(\overrightarrow {AM} .\overrightarrow {BN} = - {a^2}\)
b) Ta có: \(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} } \right)^2} = {\left( { - \frac{1}{3}\overrightarrow {BC} + \overrightarrow {BC} + \frac{5}{4}\overrightarrow {CA} } \right)^2}\)
\( = {\left( {\frac{2}{3}\overrightarrow {BC} + \frac{5}{4}\overrightarrow {CA} } \right)^2} = \frac{4}{9}B{C^2} + \frac{{25}}{{16}}A{C^2} + \frac{5}{3}\overrightarrow {BC} .\overrightarrow {CA} \)
\( = \frac{{289}}{{144}}{a^2} - \frac{5}{3}\overrightarrow {CB} .\overrightarrow {CA} = \frac{{289}}{{144}}{a^2} - \frac{5}{3}.CB.CA.\cos \widehat {BCA}\) \( = \frac{{289}}{{144}}{a^2} - \frac{5}{6}{a^2} = \frac{{169{a^2}}}{{144}}\)
\( \Rightarrow M{N^2} = \frac{{169{a^2}}}{{144}} \Rightarrow MN = \frac{{13a}}{{12}}\)