Câu hỏi: Đặt điện áp u = U0cosωt vào hai đầu đoạn mạch như hình vẽ, trong đó điện trở R và cuộn cảm thuần L không đổi, tụ điện có điện dung C thay đổi được. Sự phụ thuộc của số chỉ vôn kế V1 và V2 theo điện dung C được biểu diễn như đồ thị hình bên.
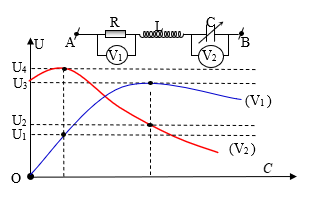
Biết U3 = 2U2. Tỉ số $\dfrac{U_{4}}{U_{1}}$ là
A. $\dfrac{3}{2}$
B. $\dfrac{4\sqrt{5}}{3}$
C. $\dfrac{4\sqrt{3}}{3}$
D. $\dfrac{5}{2}$

Biết U3 = 2U2. Tỉ số $\dfrac{U_{4}}{U_{1}}$ là
A. $\dfrac{3}{2}$
B. $\dfrac{4\sqrt{5}}{3}$
C. $\dfrac{4\sqrt{3}}{3}$
D. $\dfrac{5}{2}$
Giải 1:
+Tại vị trí cộng hưởng: $\left\{ \begin{aligned}
& {{U}_{3}}={{U}_{R\max }}=U \\
& {{Z}_{Cch}}={{Z}_{C2}}={{Z}_{L}} \\
& {{U}_{3}}=2{{U}_{2}}={{I}_{\max }}R \\
& {{U}_{2}}={{I}_{\max }}{{Z}_{C2}} \\
\end{aligned} \right.\Rightarrow {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2}$
+Tại vị trí Ucmax ta có: $\mathbf{Z}_{\mathrm{Cm}}=\dfrac{\mathbf{R}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=\dfrac{4 \mathbf{Z}_{\mathrm{L}}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=5 \mathbf{Z}_{\mathrm{L}}=\dfrac{5}{2} R$
${{U}_{4}}={{U}_{C\max }}={{U}_{AB}}\dfrac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}={{U}_{3}}\dfrac{\sqrt{{{R}^{2}}+{{\left( \dfrac{R}{2} \right)}^{2}}}}{R}={{U}_{3}}\dfrac{\sqrt{5}}{2}$
Tại Ucmax ta còn có: ${{U}_{1}}={{U}_{R}}=I.R=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-Z_{C}^{{}})}^{2}}}}=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{(\dfrac{R}{2}-\dfrac{5R}{2})}^{2}}}}=\dfrac{{{U}_{3}}}{\sqrt{5}}$
=> $\dfrac{{{U}_{4}}}{{{U}_{1}}}=\dfrac{\sqrt{5}{{U}_{3}}}{{}^{2{{U}_{3}}}/{}_{\sqrt{5}}}=\dfrac{5}{2}$
Giải 2: Chuẩn hóa:
+Tại vị trí cộng hưởng: $\left\{ \begin{aligned}
& {{U}_{3}}={{U}_{R\max }}=U \\
& {{Z}_{Cch}}={{Z}_{C2}}={{Z}_{L}} \\
& {{U}_{3}}=2{{U}_{2}}={{I}_{\max }}R \\
\end{aligned} \right.\Rightarrow {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2} $Chọn R= 2 => $ {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2}=1$
+Tại vị trí Ucmax: $\mathbf{Z}_{\mathrm{Cmax}}=\mathbf{Z}_{\mathrm{C} 1}=\dfrac{\mathbf{R}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=\dfrac{4 \mathbf{Z}_{\mathrm{L}}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=5 \mathbf{Z}_{\mathrm{L}}=\dfrac{5}{2} R=5$
+ ${{U}_{4}}={{U}_{C\max }}={{U}_{AB}}\dfrac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}={{U}_{3}}\dfrac{\sqrt{{{2}^{2}}+{{1}^{2}}}}{2}={{U}_{3}}\dfrac{\sqrt{5}}{2}$
+ ${{U}_{1}}={{U}_{R}}=I.R=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-Z_{C\max }^{{}})}^{2}}}}=\dfrac{2{{U}_{3}}}{\sqrt{{{2}^{2}}+{{(1-5)}^{2}}}}=\dfrac{{{U}_{3}}}{\sqrt{5}}$ => $\dfrac{{{U}_{4}}}{{{U}_{1}}}=\dfrac{\sqrt{5}{{U}_{3}}}{{}^{2{{U}_{3}}}/{}_{\sqrt{5}}}=\dfrac{5}{2}$
+Tại vị trí cộng hưởng: $\left\{ \begin{aligned}
& {{U}_{3}}={{U}_{R\max }}=U \\
& {{Z}_{Cch}}={{Z}_{C2}}={{Z}_{L}} \\
& {{U}_{3}}=2{{U}_{2}}={{I}_{\max }}R \\
& {{U}_{2}}={{I}_{\max }}{{Z}_{C2}} \\
\end{aligned} \right.\Rightarrow {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2}$
+Tại vị trí Ucmax ta có: $\mathbf{Z}_{\mathrm{Cm}}=\dfrac{\mathbf{R}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=\dfrac{4 \mathbf{Z}_{\mathrm{L}}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=5 \mathbf{Z}_{\mathrm{L}}=\dfrac{5}{2} R$
${{U}_{4}}={{U}_{C\max }}={{U}_{AB}}\dfrac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}={{U}_{3}}\dfrac{\sqrt{{{R}^{2}}+{{\left( \dfrac{R}{2} \right)}^{2}}}}{R}={{U}_{3}}\dfrac{\sqrt{5}}{2}$
Tại Ucmax ta còn có: ${{U}_{1}}={{U}_{R}}=I.R=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-Z_{C}^{{}})}^{2}}}}=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{(\dfrac{R}{2}-\dfrac{5R}{2})}^{2}}}}=\dfrac{{{U}_{3}}}{\sqrt{5}}$
=> $\dfrac{{{U}_{4}}}{{{U}_{1}}}=\dfrac{\sqrt{5}{{U}_{3}}}{{}^{2{{U}_{3}}}/{}_{\sqrt{5}}}=\dfrac{5}{2}$
Giải 2: Chuẩn hóa:
+Tại vị trí cộng hưởng: $\left\{ \begin{aligned}
& {{U}_{3}}={{U}_{R\max }}=U \\
& {{Z}_{Cch}}={{Z}_{C2}}={{Z}_{L}} \\
& {{U}_{3}}=2{{U}_{2}}={{I}_{\max }}R \\
\end{aligned} \right.\Rightarrow {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2} $Chọn R= 2 => $ {{Z}_{C2}}={{Z}_{L}}=\dfrac{R}{2}=1$
+Tại vị trí Ucmax: $\mathbf{Z}_{\mathrm{Cmax}}=\mathbf{Z}_{\mathrm{C} 1}=\dfrac{\mathbf{R}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=\dfrac{4 \mathbf{Z}_{\mathrm{L}}^{2}+\mathbf{Z}_{\mathrm{L}}^{2}}{\mathbf{Z}_{\mathrm{L}}}=5 \mathbf{Z}_{\mathrm{L}}=\dfrac{5}{2} R=5$
+ ${{U}_{4}}={{U}_{C\max }}={{U}_{AB}}\dfrac{\sqrt{{{R}^{2}}+Z_{L}^{2}}}{R}={{U}_{3}}\dfrac{\sqrt{{{2}^{2}}+{{1}^{2}}}}{2}={{U}_{3}}\dfrac{\sqrt{5}}{2}$
+ ${{U}_{1}}={{U}_{R}}=I.R=\dfrac{{{U}_{3}}R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-Z_{C\max }^{{}})}^{2}}}}=\dfrac{2{{U}_{3}}}{\sqrt{{{2}^{2}}+{{(1-5)}^{2}}}}=\dfrac{{{U}_{3}}}{\sqrt{5}}$ => $\dfrac{{{U}_{4}}}{{{U}_{1}}}=\dfrac{\sqrt{5}{{U}_{3}}}{{}^{2{{U}_{3}}}/{}_{\sqrt{5}}}=\dfrac{5}{2}$
Đáp án D.