Câu hỏi: Cho một đoạn mạch điện như hình bên: $R$ là biến trở; cuộn cảm thuần có độ tự cảm L thay đổi được; tụ điện có điện dung $C$, khóa $K$ và các dây nối có điện trở không đáng kể.
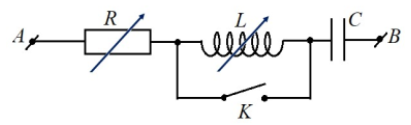
Đặt vào hai đầu AB một điện áp xoay chiều có giá trị hiệu dụng bằng $200 \mathrm{~V}$ không đổi, tần số bằng 50 Hz. Chỉnh cho $\mathrm{R}=\mathrm{R}_{0}, \mathrm{~K}$ mở, thay đổi $\mathrm{L}$ thì có hai giá trị là $\mathrm{L}_{1}=\dfrac{1}{\pi} \mathrm{H}$ và $\mathrm{L}_{2}=\dfrac{3}{\pi} \mathrm{H}$ cho cường độ dòng điện hiệu dụng trong mạch là bằng nhau. $K$ đóng, công suất tiêu thụ của mạch là 80 W và công suất tiêu thụ giảm khi $\mathrm{R}$ tăng. Đặt lại $\mathrm{R}=\mathrm{R}_{0}, \mathrm{~K}$ mở điều chỉnh $\mathrm{L}$ để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại. Giá trị của L lúc này bằng
A. $\dfrac{2,5}{\pi} \mathrm{H}$.
B. $\dfrac{10}{\pi} \mathrm{H}$.
C. $\dfrac{5}{\pi} \mathrm{H}$.
D. $\dfrac{2}{\pi} \mathrm{H}$.

Đặt vào hai đầu AB một điện áp xoay chiều có giá trị hiệu dụng bằng $200 \mathrm{~V}$ không đổi, tần số bằng 50 Hz. Chỉnh cho $\mathrm{R}=\mathrm{R}_{0}, \mathrm{~K}$ mở, thay đổi $\mathrm{L}$ thì có hai giá trị là $\mathrm{L}_{1}=\dfrac{1}{\pi} \mathrm{H}$ và $\mathrm{L}_{2}=\dfrac{3}{\pi} \mathrm{H}$ cho cường độ dòng điện hiệu dụng trong mạch là bằng nhau. $K$ đóng, công suất tiêu thụ của mạch là 80 W và công suất tiêu thụ giảm khi $\mathrm{R}$ tăng. Đặt lại $\mathrm{R}=\mathrm{R}_{0}, \mathrm{~K}$ mở điều chỉnh $\mathrm{L}$ để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại. Giá trị của L lúc này bằng
A. $\dfrac{2,5}{\pi} \mathrm{H}$.
B. $\dfrac{10}{\pi} \mathrm{H}$.
C. $\dfrac{5}{\pi} \mathrm{H}$.
D. $\dfrac{2}{\pi} \mathrm{H}$.
$\omega =2\pi f=2\pi .50=100\pi $ (rad/s)
${{Z}_{L}}=\omega L\Rightarrow {{Z}_{L1}}=100\pi .\dfrac{1}{\pi }=100\Omega $ và ${{Z}_{L2}}=100\pi .\dfrac{3}{\pi }=300\Omega $
K mở thì $I=\dfrac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\xrightarrow{{{I}_{1}}={{I}_{2}}}{{Z}_{C}}=\dfrac{{{Z}_{L1}}+{{Z}_{L2}}}{2}=\dfrac{100+300}{2}=200\Omega $
K đóng thì $P=\dfrac{{{U}^{2}}R}{{{R}^{2}}+Z_{C}^{2}}\Rightarrow 80=\dfrac{{{200}^{2}}R}{{{R}^{2}}+{{200}^{2}}}\Rightarrow \left[ \begin{aligned}
& R=400\Omega (TM) \\
& R=100\Omega (loai) \\
\end{aligned} \right.$
K mở thì ${{Z}_{L}}={{Z}_{C}}+\dfrac{{{R}^{2}}}{{{Z}_{C}}}=200+\dfrac{{{400}^{2}}}{200}=1000\Omega \to L=\dfrac{{{Z}_{L}}}{\omega }=\dfrac{1000}{100\pi }=\dfrac{10}{\pi }H$.
${{Z}_{L}}=\omega L\Rightarrow {{Z}_{L1}}=100\pi .\dfrac{1}{\pi }=100\Omega $ và ${{Z}_{L2}}=100\pi .\dfrac{3}{\pi }=300\Omega $
K mở thì $I=\dfrac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\xrightarrow{{{I}_{1}}={{I}_{2}}}{{Z}_{C}}=\dfrac{{{Z}_{L1}}+{{Z}_{L2}}}{2}=\dfrac{100+300}{2}=200\Omega $
K đóng thì $P=\dfrac{{{U}^{2}}R}{{{R}^{2}}+Z_{C}^{2}}\Rightarrow 80=\dfrac{{{200}^{2}}R}{{{R}^{2}}+{{200}^{2}}}\Rightarrow \left[ \begin{aligned}
& R=400\Omega (TM) \\
& R=100\Omega (loai) \\
\end{aligned} \right.$
K mở thì ${{Z}_{L}}={{Z}_{C}}+\dfrac{{{R}^{2}}}{{{Z}_{C}}}=200+\dfrac{{{400}^{2}}}{200}=1000\Omega \to L=\dfrac{{{Z}_{L}}}{\omega }=\dfrac{1000}{100\pi }=\dfrac{10}{\pi }H$.
Đáp án B.