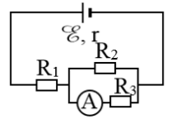
Câu hỏi: Cho mạch điện có sơ đồ như hình bên: $E=12V;{{R}_{1}}=4\Omega ;{{R}_{2}}={{R}_{3}}=10\Omega $. Bỏ qua điện trở của ampe kế A và dây nối. Số chỉ của ampe kế là $0,6A$. Giá trị điện trở trong r của nguồn điện là
A. $.1,2\Omega $
B. 1,6Ω
C. 0,5Ω
D. 1Ω

A. $.1,2\Omega $
B. 1,6Ω
C. 0,5Ω
D. 1Ω
Phương pháp:
Định luật Ôm đối với toàn mạch: $I=\dfrac{E}{{{R}_{N}}+r}$
Đối với đoạn mạch mắc nối tiếp: $\left\{ \begin{aligned}
& {{R}_{nt}}={{R}_{1}}+{{R}_{2}} \\
& I={{I}_{1}}+{{I}_{2}} \\
& U={{U}_{1}}+{{U}_{2}} \\
\end{aligned} \right.$
Đối với đoạn mạch mắc song song: $\left\{ \begin{aligned}
& {{R}_{//}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}} \\
& I={{I}_{1}}+{{I}_{2}} \\
& U={{U}_{1}}={{U}_{2}} \\
\end{aligned} \right.$
Cách giải:
Mạch ngoài gồm: ${{R}_{1}}nt\left( {{R}_{2}}//{{R}_{3}} \right)$
Điện trở tương đương của mạch ngoài là: ${{R}_{N}}={{R}_{1}}+{{R}_{23}}={{R}_{1}}+\dfrac{{{R}_{2}}{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}}=4+\dfrac{10.10}{10+10}=9\Omega $
Số chỉ của ampe kế là $0,6A\Rightarrow {{I}_{3}}=0,6A\Rightarrow {{U}_{3}}={{I}_{3}}{{R}_{3}}=0,6.10=6V$
Do ${{R}_{1}} nt \left( {{R}_{2}}//{{R}_{3}} \right)\Rightarrow {{U}_{23}}=6V\Rightarrow {{I}_{23}}=\dfrac{{{U}_{23}}}{{{R}_{23}}}=\dfrac{6}{5}=1,2A\Rightarrow I={{I}_{23~}}=1,2A$
Áp dụng định luật Ôm cho toàn mạch ta có:
$I=\dfrac{E}{{{R}_{N}}+r}\Leftrightarrow 1,2=\dfrac{12}{9+r}\Leftrightarrow 9+r=10\Rightarrow r=1\Omega $
Định luật Ôm đối với toàn mạch: $I=\dfrac{E}{{{R}_{N}}+r}$
Đối với đoạn mạch mắc nối tiếp: $\left\{ \begin{aligned}
& {{R}_{nt}}={{R}_{1}}+{{R}_{2}} \\
& I={{I}_{1}}+{{I}_{2}} \\
& U={{U}_{1}}+{{U}_{2}} \\
\end{aligned} \right.$
Đối với đoạn mạch mắc song song: $\left\{ \begin{aligned}
& {{R}_{//}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}} \\
& I={{I}_{1}}+{{I}_{2}} \\
& U={{U}_{1}}={{U}_{2}} \\
\end{aligned} \right.$
Cách giải:
Mạch ngoài gồm: ${{R}_{1}}nt\left( {{R}_{2}}//{{R}_{3}} \right)$
Điện trở tương đương của mạch ngoài là: ${{R}_{N}}={{R}_{1}}+{{R}_{23}}={{R}_{1}}+\dfrac{{{R}_{2}}{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}}=4+\dfrac{10.10}{10+10}=9\Omega $
Số chỉ của ampe kế là $0,6A\Rightarrow {{I}_{3}}=0,6A\Rightarrow {{U}_{3}}={{I}_{3}}{{R}_{3}}=0,6.10=6V$
Do ${{R}_{1}} nt \left( {{R}_{2}}//{{R}_{3}} \right)\Rightarrow {{U}_{23}}=6V\Rightarrow {{I}_{23}}=\dfrac{{{U}_{23}}}{{{R}_{23}}}=\dfrac{6}{5}=1,2A\Rightarrow I={{I}_{23~}}=1,2A$
Áp dụng định luật Ôm cho toàn mạch ta có:
$I=\dfrac{E}{{{R}_{N}}+r}\Leftrightarrow 1,2=\dfrac{12}{9+r}\Leftrightarrow 9+r=10\Rightarrow r=1\Omega $
Đáp án D.