Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a\sqrt{3},SA$ vuông góc với mặt phẳng đáy và $SA=a\sqrt{2}$ (minh họa như hình bên dưới).
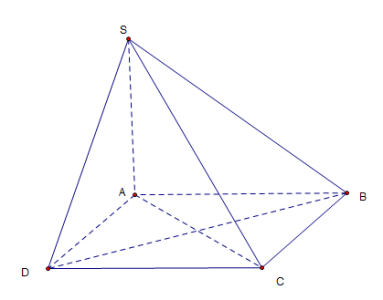
Khoảng cách từ $B$ đến mặt phẳng $\left( SCD \right)$ bằng
A. $\dfrac{a\sqrt{6}}{6}.$
B. $\dfrac{a\sqrt{30}}{5}.$
C. $\dfrac{a\sqrt{5}}{6}.$
D. $\dfrac{a\sqrt{30}}{6}.$

$\left\{ \begin{aligned}
& AB//CD \\
& AB\not\subset \left( SCD \right) \\
\end{aligned} \right.\Rightarrow AB//\left( SCD \right).$
$\left\{ \begin{aligned}
& \left( SCD \right)\bot \left( SAD \right) \\
& \left( SCD \right)\cap \left( SAD \right)=SD \\
\end{aligned} \right. $ kẻ $ AH\bot SD=\left\{ H \right\}\Rightarrow d\left( B,\left( SCD \right) \right)=d\left( A,\left( SCD \right) \right)=AH.$
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=\sqrt{{{\left( a\sqrt{2} \right)}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}}=a\sqrt{5}.$
$\Delta SAD\bot A:AH.SD=SA.AD\Leftrightarrow AH=\dfrac{SA.AD}{SD}=\dfrac{a\sqrt{2}.a\sqrt{3}}{a\sqrt{5}}=\dfrac{a\sqrt{30}}{5}$

Khoảng cách từ $B$ đến mặt phẳng $\left( SCD \right)$ bằng
A. $\dfrac{a\sqrt{6}}{6}.$
B. $\dfrac{a\sqrt{30}}{5}.$
C. $\dfrac{a\sqrt{5}}{6}.$
D. $\dfrac{a\sqrt{30}}{6}.$
$\left\{ \begin{aligned}
& AB//CD \\
& AB\not\subset \left( SCD \right) \\
\end{aligned} \right.\Rightarrow AB//\left( SCD \right).$
$\left\{ \begin{aligned}
& \left( SCD \right)\bot \left( SAD \right) \\
& \left( SCD \right)\cap \left( SAD \right)=SD \\
\end{aligned} \right. $ kẻ $ AH\bot SD=\left\{ H \right\}\Rightarrow d\left( B,\left( SCD \right) \right)=d\left( A,\left( SCD \right) \right)=AH.$
$SD=\sqrt{S{{A}^{2}}+A{{D}^{2}}}=\sqrt{{{\left( a\sqrt{2} \right)}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}}=a\sqrt{5}.$
$\Delta SAD\bot A:AH.SD=SA.AD\Leftrightarrow AH=\dfrac{SA.AD}{SD}=\dfrac{a\sqrt{2}.a\sqrt{3}}{a\sqrt{5}}=\dfrac{a\sqrt{30}}{5}$
Đáp án B.