Câu hỏi: Một viên đạn được bắn lên trời từ một vị trí cách mặt đất 1000m theo phương thẳng đứng với vận tốc ban đầu \({v_0} = 245m/s\) (bỏ qua sức cản không khí) .
Giải chi tiết:
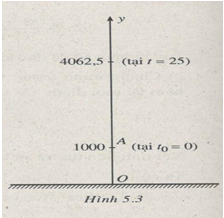
Chọn Oy theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc O ở mặt đất và A là vị trí viên đạn được bắn lên, gốc thời gian (từ lúc t = 0) được tính từ vị trí A (h. 5.3); khi đó chuyển động của viên đạn là chuyển động biến đổi với vận tốc ban đầu và với gia tốc \(g = - 9,8 m/{s^2}\). (Gia tốc nhận giá trị âm vì vecto gia tốc ngược chiều dương của trục Oy). Phương trình chuyển động của viên đạn là
\(y = 1000 + 245t - 4,9{t^2}\)
Ta có \(v\left( t \right) = y' = 245 - 9,8t\)
Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi khi
\(v\left( t \right) = 0 \Leftrightarrow 245 - 9,8t = 0 \Leftrightarrow t = 25 \left(s \right)\)
Khi đó viên đạn cách mặt đất là
\(y\left( {25} \right) = 1000 + 245.25 - 4,{9.25^2} = 4062,5 \left(m \right)\)
Giải chi tiết:
Viên đạn rơi đến đất khi \(y = 0\). Vậy nếu gọi \({t_1}\) là thời gian kể từ khi viên đạn được bắn lên trời đến khi nó rơi tới đất thì \({t_1}\) phải là nghiệm dương của phương trình.
\(0 = 1000 + 245t - 4,9{t^2} \Leftrightarrow {t_1} = 54 \left( s \right)\)
Câu a
Tìm thời điểm \({t_0}\) tại đó viên đạn đạt tốc độ cao nhất và sẽ bắt đầu rơi. Khi đó viên đạn cách mặt đất bao nhiêu mét?Giải chi tiết:
Chọn Oy theo phương thẳng đứng, chiều dương hướng từ mặt đất lên trời, gốc O ở mặt đất và A là vị trí viên đạn được bắn lên, gốc thời gian (từ lúc t = 0) được tính từ vị trí A (h. 5.3); khi đó chuyển động của viên đạn là chuyển động biến đổi với vận tốc ban đầu và với gia tốc \(g = - 9,8 m/{s^2}\). (Gia tốc nhận giá trị âm vì vecto gia tốc ngược chiều dương của trục Oy). Phương trình chuyển động của viên đạn là
\(y = 1000 + 245t - 4,9{t^2}\)
Ta có \(v\left( t \right) = y' = 245 - 9,8t\)
Viên đạn đạt độ cao lớn nhất và sẽ bắt đầu rơi khi
\(v\left( t \right) = 0 \Leftrightarrow 245 - 9,8t = 0 \Leftrightarrow t = 25 \left(s \right)\)
Khi đó viên đạn cách mặt đất là
\(y\left( {25} \right) = 1000 + 245.25 - 4,{9.25^2} = 4062,5 \left(m \right)\)
Câu b
Sau bak nhiêu giây (kể từ lúc bắn), viên đạn rơi xuống mặt đất?Giải chi tiết:
Viên đạn rơi đến đất khi \(y = 0\). Vậy nếu gọi \({t_1}\) là thời gian kể từ khi viên đạn được bắn lên trời đến khi nó rơi tới đất thì \({t_1}\) phải là nghiệm dương của phương trình.
\(0 = 1000 + 245t - 4,9{t^2} \Leftrightarrow {t_1} = 54 \left( s \right)\)

Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!