Câu hỏi: Trên mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O có bán kính R (R > 0). Trên các tia Ox và Oy lần lượt lấy hai điểm A và B sao cho đường thẳng AB luôn tiếp xúc với đường tròn đó.
Hãy xác định tọa độ của A và B để tam giác OAB có diện tích nhỏ nhất.
Hãy xác định tọa độ của A và B để tam giác OAB có diện tích nhỏ nhất.
Lời giải chi tiết
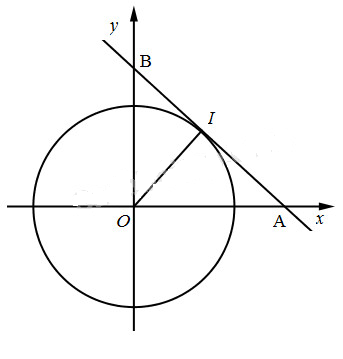
Ta có
\(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}OI. AB = \dfrac{{\rm{R}}}{2}. AB;\\AB = IA + IB \ge 2\sqrt {IA. IB} = 2\sqrt {{\rm{O}}{I^2}} = 2{\rm{R}};\\AB = 2{\rm{R}} \Leftrightarrow IA = IB = R.\end{array}\)
Lúc đó tam giác OAB vuông cân tại O,
Cạnh huyền \(AB = 2R.\)
\(OA = OB = R\sqrt 2 \)
Suy ra \({S_{OAB}} \ge \dfrac{{\rm{R}}}{2}. 2{\rm{R}} = {R^2}.\)
Vậy \({S_{OAB}}\) nhỏ nhất bằng \({R^2}\) khi \(OA = OB = R\sqrt 2 .\) Khi đó tọa độ \(A\left( {{\rm{R}}\sqrt 2; 0} \right)\) và \(B\left( {0; R\sqrt 2 } \right).\)
Ta có
\(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}OI. AB = \dfrac{{\rm{R}}}{2}. AB;\\AB = IA + IB \ge 2\sqrt {IA. IB} = 2\sqrt {{\rm{O}}{I^2}} = 2{\rm{R}};\\AB = 2{\rm{R}} \Leftrightarrow IA = IB = R.\end{array}\)
Lúc đó tam giác OAB vuông cân tại O,
Cạnh huyền \(AB = 2R.\)
\(OA = OB = R\sqrt 2 \)
Suy ra \({S_{OAB}} \ge \dfrac{{\rm{R}}}{2}. 2{\rm{R}} = {R^2}.\)
Vậy \({S_{OAB}}\) nhỏ nhất bằng \({R^2}\) khi \(OA = OB = R\sqrt 2 .\) Khi đó tọa độ \(A\left( {{\rm{R}}\sqrt 2; 0} \right)\) và \(B\left( {0; R\sqrt 2 } \right).\)