Câu hỏi:
Phương pháp giải:
Áp dụng công thức ΔV = V0βΔt = V03αΔt
Lời giải chi tiết:
Độ nở khối (thể tích) của sắt được tính theo công thức :
ΔV = V0βΔt = V03αΔt
với V0 là thể tích của khối sắt ở 0°C, β = 3α là hệ số nở khối của sắt, còn độ tăng nhiệt độ Δt của khối sắt liên hệ với lượng nhiệt Q mà khối sắt đã hấp thụ khi bị nung nóng bởi công thức :
Q = cmΔt ≈cDV0Δt với c là nhiột dung riêng, D là khối lượng riêng và m là khối lượng của sắt. Vì D = D0(1 + βt), nhưng βt << 1 nên coi gần đúng : m = D0V0 ≈ DV0.
Từ đó suy ra: \(\Delta V = {{3\alpha Q} \over {cD}}\)
Thay số ta được:
\(\Delta V = {{{{3.11.10}^{ - 6}}{{. 297.10}^3}} \over {460.7800}} \approx 2,{73.10^{ - 6}}{m^3} = 2,73c{m^3}\)
Phương pháp giải:
Áp dụng công thức Fc = σ(πD + πd) ≈ σ2πD
Lời giải chi tiết:
Muốn kéo vòng nhôm bứt khỏi mặt thoáng của nước thì cần tác dụng lên nó lực F hướng thẳng đứng lên trên và có cường độ nhỏ nhất bằng tổng trọng lực P của vòng nhôm và lực căng bề mặt Fc của nước :
F = P + Fc
Vì mặt nước tiếp xúc với cả mặt trong và mặt ngoài của vòng nhôm nên lực căng bề mặt Fc có độ lớn bằng :
Fc = σ(πD + πd) ≈ σ2πD
với D là đường kính ngoài và d là đường kính trong của vòng nhôm mỏng. Bỏ qua độ dày của vòng nhôm và coi gần đúng :
d ≈ D hay D + d ≈ 2D.
Từ đó suy ra: F≈ P + π2πD.
Thay số, ta tìm được :
F = 5,7.10-3. 9,8 + 72.10-3. 2.3,14.40.10-3 ≈ 74.10-3 N.
Phương pháp giải:
Áp dụng công thức Q1 = c1m(t0 - t1)
Lời giải chi tiết:
Lượng nhiệt cần cung cấp để biến đổi m = 6,0 kg nước đá ở nhiệt độ t1 = -20°C biến thành hơi nước ở t2 = 100°C có giá trị bằng :
Q = Q1 + Q2 + Q3 + Q4
trong đó lượng nhiệt Q1 = c1m(t0 - t1) cung cấp cho m (kg) nước đá có
nhiệt dung riêng cđ để nhiệt độ của nó tăng từ t1 = -20°C đến t0 = 0°C; lượng
nhiệt Q0 = λm cung cấp cho m (kg) nước đá có nhiệt nóng chảy riêng λ ở
t0 = 0°C tan thành nước ở cùng nhiệt độ; lượng nhiệt Q2= c0m(t2 -t0)
cung cấp cho m (kg) nước có nhiệt dung riêng cn để nhiệt độ của nó tăng từ t0 = 0°C đến t2 = 100°C; lượng nhiệt Q3 = Lm cung cấp cho m (kg) nước
có nhiệt hoá hơi riêng L ở t2 = 100°C biến thành hơi nước ở cùng nhiệt độ. Như vậy, ta có thể viết:
Q = cđm(t0 - t1) + λm + cnm(t2 -t0) + Lm
hay Q = m[cđ(t0 - t1) + λ + cn(t2 -t0) + L]
Thay số, ta tìm được :
Q = 6,0. [2090.(0 + 20) + 3,4.105 + 4180.(100-0) + 2,3.106]
Q ≈ 186.106 J.
Phương pháp giải:
Áp dụng công thức \(M = A. V\)
Lời giải chi tiết:
Vì độ ẩm cực đại A20 của không khí ở 200C có giá trị bằng khối lượng riêng của hơi nước bão hoà ở cùng nhiệt độ, nên ta có : A20 = 17,30 g/m3.
và suy ra lượng hơi nước cực đại có trong thể tích V = 2,0.1010 m3 của đám mây :
M20 = A20V = 17,30.10-3. 2,0.1010 = 3,46.108 kg
Khi nhiệt độ không khí của đám mây giảm xuống tới 10°C thì lượng hơi nước cực đại có trong thể tích V = 2,0.1010 m3 của đám mây chỉ còn bằng :
M10 = A10V = 9,40.10-3. 2,0.1010 = l, 88.108 kg. Như vậy khối lượng nước mưa rơi xuống bằng :
M = M20 - M10 = 3,46.108- l, 88.108 = 1,58.108 kg = 158.103 tấn.
Phương pháp giải:
Áp dụng công thức định luật Húc \({F_1} = {E_1}{S \over {{l_0}}}\Delta {l_1}\)
Lời giải chi tiết:
Giả sử vật nặng được treo tại vị trí cách đầu B của thanh rắn một đoạn x. Khi đó ta có thể phân tích trọng lực \(\overrightarrow P \) tác dụng lên vật nặng thành hai lực thành phần \(\overrightarrow F_1 \) và \(\overrightarrow F_2 \) song song với. Lực tác dụng lên sợi dây thép tại điểm B và làm sợi dây thép dãn dài thêm một đoạn Δl1, lực \(\overrightarrow F_2 \) tác dụng lên sợi dây đồng tại điểm D và làm sợi dây đồng dãn dài thêm một đoạn Δl2. Vì sợi dây thép và sợi dây đồng có độ dài ban đầu l0 và tiết diện S giống nhau, nên theo định luật Húc, ta có :
\({F_1} = {E_1}{S \over {{l_0}}}\Delta {l_1}\) và \({F_2} = {E_2}{S \over {{l_0}}}\Delta {l_2}\)
Muốn thanh rắn BD nằm ngang thì sợi dây thép và sợi dây đồng phải có độ dãn dài bằng nhau: Δl1 = Δl2. Thay điều kiện này vào F1 và F2 , ta được :
\({{{F_1}} \over {{F_2}}} = {{{E_1}} \over {{E_2}}}\)
Mặt khác theo quy tắc tổng hợp hai lực song song cùng chiều, ta có :
\({{{F_1}} \over {{F_2}}} = {{a - x} \over a}\)
Từ đó, ta suy ra : \(x = {{{E_2}a} \over {{E_1} + {E_2}}} = {{11,{{7.10}^{10}}. 0,80} \over {19,{{6.10}^{10}} + 11,{{7.10}^{10}}}} \approx 30\left( {cm} \right)\)
VII. 6.
Một khối sắt hình lập phương bị nung nóng và hấp thụ lượng nhiệt 297 kJ. Xác định độ tăng thể tích của khối sắt. Cho biết sắt (ở 20°C) có khối lượng riêng là 7800 kg/m3, nhiệt dung riêng là 460 J/kg. K và hệ số nở dài là 11.10-6 K-1.Phương pháp giải:
Áp dụng công thức ΔV = V0βΔt = V03αΔt
Lời giải chi tiết:
Độ nở khối (thể tích) của sắt được tính theo công thức :
ΔV = V0βΔt = V03αΔt
với V0 là thể tích của khối sắt ở 0°C, β = 3α là hệ số nở khối của sắt, còn độ tăng nhiệt độ Δt của khối sắt liên hệ với lượng nhiệt Q mà khối sắt đã hấp thụ khi bị nung nóng bởi công thức :
Q = cmΔt ≈cDV0Δt với c là nhiột dung riêng, D là khối lượng riêng và m là khối lượng của sắt. Vì D = D0(1 + βt), nhưng βt << 1 nên coi gần đúng : m = D0V0 ≈ DV0.
Từ đó suy ra: \(\Delta V = {{3\alpha Q} \over {cD}}\)
Thay số ta được:
\(\Delta V = {{{{3.11.10}^{ - 6}}{{. 297.10}^3}} \over {460.7800}} \approx 2,{73.10^{ - 6}}{m^3} = 2,73c{m^3}\)
VII. 7.
Một vòng nhôm mỏng khối lượng 5,7 g được treo vào một lực kế lò xo và mặt đáy của vòng nhôm đặt tiếp xúc với mặt nước đựng trong cốc thủy tinh. Đường kính ngoài của vòng nhôm bằng 40 mm. Cho biết hệ số căng bề mặt của nước là 72.10-3 N/m. Bỏ qua độ dày của vòng nhôm. Lấy g = 9,8 m/s2. Xác định lực kéo vòng nhôm để có thể bứt nó lên khỏi mặt nước.Phương pháp giải:
Áp dụng công thức Fc = σ(πD + πd) ≈ σ2πD
Lời giải chi tiết:
Muốn kéo vòng nhôm bứt khỏi mặt thoáng của nước thì cần tác dụng lên nó lực F hướng thẳng đứng lên trên và có cường độ nhỏ nhất bằng tổng trọng lực P của vòng nhôm và lực căng bề mặt Fc của nước :
F = P + Fc
Vì mặt nước tiếp xúc với cả mặt trong và mặt ngoài của vòng nhôm nên lực căng bề mặt Fc có độ lớn bằng :
Fc = σ(πD + πd) ≈ σ2πD
với D là đường kính ngoài và d là đường kính trong của vòng nhôm mỏng. Bỏ qua độ dày của vòng nhôm và coi gần đúng :
d ≈ D hay D + d ≈ 2D.
Từ đó suy ra: F≈ P + π2πD.
Thay số, ta tìm được :
F = 5,7.10-3. 9,8 + 72.10-3. 2.3,14.40.10-3 ≈ 74.10-3 N.
VII. 8.
Xác định lượng nhiệt cần cung cấp để biến đổi 6,0 kg nước đá ở - 200C thành hơi nước ở 1000C. Cho biết nước đá có nhiệt dung riêng là 2090 J/kg. K và nhiệt nóng chảy riêng là 3,4.105 J/kg, nước có nhiệt dung riêng là 4180 J/kg. K và nhiệt hóa hơi riêng là 2,3.106 J/kg. Bỏ qua sự mất mát nhiệt do bình chứa hấp thụ và do truyền ra bên ngoài.Phương pháp giải:
Áp dụng công thức Q1 = c1m(t0 - t1)
Lời giải chi tiết:
Lượng nhiệt cần cung cấp để biến đổi m = 6,0 kg nước đá ở nhiệt độ t1 = -20°C biến thành hơi nước ở t2 = 100°C có giá trị bằng :
Q = Q1 + Q2 + Q3 + Q4
trong đó lượng nhiệt Q1 = c1m(t0 - t1) cung cấp cho m (kg) nước đá có
nhiệt dung riêng cđ để nhiệt độ của nó tăng từ t1 = -20°C đến t0 = 0°C; lượng
nhiệt Q0 = λm cung cấp cho m (kg) nước đá có nhiệt nóng chảy riêng λ ở
t0 = 0°C tan thành nước ở cùng nhiệt độ; lượng nhiệt Q2= c0m(t2 -t0)
cung cấp cho m (kg) nước có nhiệt dung riêng cn để nhiệt độ của nó tăng từ t0 = 0°C đến t2 = 100°C; lượng nhiệt Q3 = Lm cung cấp cho m (kg) nước
có nhiệt hoá hơi riêng L ở t2 = 100°C biến thành hơi nước ở cùng nhiệt độ. Như vậy, ta có thể viết:
Q = cđm(t0 - t1) + λm + cnm(t2 -t0) + Lm
hay Q = m[cđ(t0 - t1) + λ + cn(t2 -t0) + L]
Thay số, ta tìm được :
Q = 6,0. [2090.(0 + 20) + 3,4.105 + 4180.(100-0) + 2,3.106]
Q ≈ 186.106 J.
VII. 9.
Một đám mây thể tích 2,0.1010 m3 chứa hơi nước bão hòa trong khí quyển ở nhiệt độ 200C. Khi nhiệt độ của đám mây giảm xuống tới 100C, hơi nước bão hòa trong đám mây tụ lại thành các hạt mưa. Xác định khối lượng nước mưa rơi xuống. Cho biết khối lượng riêng của hơi nước bão hòa trong không khí ở 100C là 9,40 g/m3 và ở 200C là 17,30 g/m3.Phương pháp giải:
Áp dụng công thức \(M = A. V\)
Lời giải chi tiết:
Vì độ ẩm cực đại A20 của không khí ở 200C có giá trị bằng khối lượng riêng của hơi nước bão hoà ở cùng nhiệt độ, nên ta có : A20 = 17,30 g/m3.
và suy ra lượng hơi nước cực đại có trong thể tích V = 2,0.1010 m3 của đám mây :
M20 = A20V = 17,30.10-3. 2,0.1010 = 3,46.108 kg
Khi nhiệt độ không khí của đám mây giảm xuống tới 10°C thì lượng hơi nước cực đại có trong thể tích V = 2,0.1010 m3 của đám mây chỉ còn bằng :
M10 = A10V = 9,40.10-3. 2,0.1010 = l, 88.108 kg. Như vậy khối lượng nước mưa rơi xuống bằng :
M = M20 - M10 = 3,46.108- l, 88.108 = 1,58.108 kg = 158.103 tấn.
VII. 10.
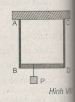
Một sợi dây thép AB và một sợi dây đồng CD có độ dài và tiết diện giống nhau. Đầu trên của mỗi dây được treo cố định vào giá đỡ tại hai điểm A và C, đầu dưới của chúng được buộc vào hai đầu B và D của một thanh rắn nằm ngang dài 0,80 m (Hình VII). Hỏi phải treo vật nặng P tại vị trí nào trên thanh BD để thanh này luôn nằm ngang? Cho biết suất đàn hồi của thép là E1 = 19,6.1010 Pa, của đồng là E2 = 11,7.1010Pa. Giả thiết thành rắn BD không bị biến dạng.
Phương pháp giải:
Áp dụng công thức định luật Húc \({F_1} = {E_1}{S \over {{l_0}}}\Delta {l_1}\)
Lời giải chi tiết:
Giả sử vật nặng được treo tại vị trí cách đầu B của thanh rắn một đoạn x. Khi đó ta có thể phân tích trọng lực \(\overrightarrow P \) tác dụng lên vật nặng thành hai lực thành phần \(\overrightarrow F_1 \) và \(\overrightarrow F_2 \) song song với. Lực tác dụng lên sợi dây thép tại điểm B và làm sợi dây thép dãn dài thêm một đoạn Δl1, lực \(\overrightarrow F_2 \) tác dụng lên sợi dây đồng tại điểm D và làm sợi dây đồng dãn dài thêm một đoạn Δl2. Vì sợi dây thép và sợi dây đồng có độ dài ban đầu l0 và tiết diện S giống nhau, nên theo định luật Húc, ta có :
\({F_1} = {E_1}{S \over {{l_0}}}\Delta {l_1}\) và \({F_2} = {E_2}{S \over {{l_0}}}\Delta {l_2}\)
Muốn thanh rắn BD nằm ngang thì sợi dây thép và sợi dây đồng phải có độ dãn dài bằng nhau: Δl1 = Δl2. Thay điều kiện này vào F1 và F2 , ta được :
\({{{F_1}} \over {{F_2}}} = {{{E_1}} \over {{E_2}}}\)
Mặt khác theo quy tắc tổng hợp hai lực song song cùng chiều, ta có :
\({{{F_1}} \over {{F_2}}} = {{a - x} \over a}\)
Từ đó, ta suy ra : \(x = {{{E_2}a} \over {{E_1} + {E_2}}} = {{11,{{7.10}^{10}}. 0,80} \over {19,{{6.10}^{10}} + 11,{{7.10}^{10}}}} \approx 30\left( {cm} \right)\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!