Câu hỏi: Cho tứ diện đều ABCD cạnh a. Diện tích xung quanh của hình trụ có đáy là đường tròn nội tiếp tam giác BCD, chiều cao bằng chiều cao của tứ diện ABCD là
A. ${{\pi {a^2}\sqrt 3 } \over 2}$
B. ${{\pi {a^2}\sqrt 2 } \over 3}$
C. ${{\pi {a^2}\sqrt 3 } \over 3}$
D. ${{\pi {a^2}\sqrt 2 } \over 2}$
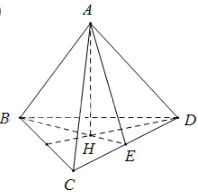
Bán kính đáy hình trụ:
\(R = HE = \frac{1}{3}BE\) \(= \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\)
\(BH = \frac{2}{3}BE = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Chiều cao hình trụ:
\(\begin{array}{l}h = AH = \sqrt {A{B^2} - B{H^2}} \\ = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\end{array}\)
\(\Rightarrow {S_{xq}} = 2\pi Rh\) \(= 2\pi .\frac{{a\sqrt 3 }}{6}.\frac{{a\sqrt 6 }}{3} = \frac{{\pi {a^2}\sqrt 2 }}{3}\)
A. ${{\pi {a^2}\sqrt 3 } \over 2}$
B. ${{\pi {a^2}\sqrt 2 } \over 3}$
C. ${{\pi {a^2}\sqrt 3 } \over 3}$
D. ${{\pi {a^2}\sqrt 2 } \over 2}$
Bán kính đáy hình trụ:
\(R = HE = \frac{1}{3}BE\) \(= \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\)
\(BH = \frac{2}{3}BE = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Chiều cao hình trụ:
\(\begin{array}{l}h = AH = \sqrt {A{B^2} - B{H^2}} \\ = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\end{array}\)
\(\Rightarrow {S_{xq}} = 2\pi Rh\) \(= 2\pi .\frac{{a\sqrt 3 }}{6}.\frac{{a\sqrt 6 }}{3} = \frac{{\pi {a^2}\sqrt 2 }}{3}\)
Đáp án B.