Câu hỏi: Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0
B. 1
C. 2
D. Vô số
A. 0
B. 1
C. 2
D. Vô số
Lời giải chi tiết
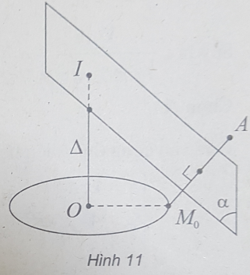
Lấy điểm M0 cố định trên đường tròn (C).
Gọi (α) là mặt phẳng trung trực của AM0 và đường thẳng Δ là trục của (C)
Ta có: I = (α) ∩ Δ là tâm mặt cầu thỏa mãn yêu cầu đề bài.
Nhận xét: Tâm I là duy nhất. Thật vậy, giả sử M nằm trên đường tròn (C) khác với M0
Gọi (α') là mặt phẳng trung trực của AM và I' = (α') ∩ Δ
Khi đó, mặt cầu tâm I' thỏa mãn yêu cầu đề bài.
Ta có: I'A = I'M = I'M0 cho ta I' thuộc mặt phẳng trung trực (α) của AM0
Suy ra: I' = (α) ∩ Δ
Vậy I' ≡ I
Lấy điểm M0 cố định trên đường tròn (C).
Gọi (α) là mặt phẳng trung trực của AM0 và đường thẳng Δ là trục của (C)
Ta có: I = (α) ∩ Δ là tâm mặt cầu thỏa mãn yêu cầu đề bài.
Nhận xét: Tâm I là duy nhất. Thật vậy, giả sử M nằm trên đường tròn (C) khác với M0
Gọi (α') là mặt phẳng trung trực của AM và I' = (α') ∩ Δ
Khi đó, mặt cầu tâm I' thỏa mãn yêu cầu đề bài.
Ta có: I'A = I'M = I'M0 cho ta I' thuộc mặt phẳng trung trực (α) của AM0
Suy ra: I' = (α) ∩ Δ
Vậy I' ≡ I
Đáp án B.