Câu hỏi: 1. Vectơ chỉ phương của đường thẳng
Định nghĩa :
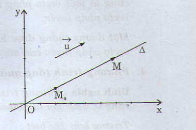
vectơ \(\vec{u}\) được gọi là vectơ chỉ phương của đường thẳng \(∆\) nếu \(\vec{u}\) ≠ \(\vec{0}\) và giá của \(\vec{u}\) song song hoặc trùng với \(∆\)
Nhận xét :
- Nếu \(\vec{u}\) là một vectơ chỉ phương của đường thẳng \(∆\) thì \(k\vec{u} ( k≠ 0)\) cũng là một vectơ chỉ phương của \(∆\) , do đó một đường thẳng có vô số vectơ chỉ phương.
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó.
2. Phương trình tham số của đường thẳng
- Phương trình tham số của đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ; y_0)\) và nhận vectơ \(\vec{u} = (u_1; u_2)\) làm vectơ chỉ phương là :
\(∆\) : \(\left\{\begin{matrix} x= x_{0}+tu_{1}& \\ y= y_{0}+tu_{2}& \end{matrix}\right.\)
-Khi \(u_1≠ 0\) thì tỉ số \(k= \dfrac{u_{2}}{u_{1}}\) được gọi là hệ số góc của đường thẳng.
Từ đây, ta có phương trình đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ; y_0)\) và có hệ số góc k là:
\(y – y_0 = k(x – x_0)\)
Chú ý: Ta đã biết hệ số góc \(k = \tan α\) với góc \(α\) là góc của đường thẳng \(∆\) hợp với chiều dương của trục \(Ox\)
3. Vectơ pháp tuyến của đường thẳng
Định nghĩa: Vectơ \(\vec{n}\) được gọi là vectơ pháp tuyến của đường thẳng \(∆\) nếu \(\vec{n}\) ≠ \(\vec{0}\) và \(\vec{n}\) vuông góc với vectơ chỉ phương của \(∆\)
Nhận xét:
- Nếu \(\vec{n}\) là một vectơ pháp tuyến của đường thẳng \(∆\) thì k\(\vec{n}\) \((k ≠ 0)\) cũng là một vectơ pháp tuyến của \(∆\), do đó một đường thẳng có vô số vec tơ pháp tuyến.
- Một đường thẳng được hoàn toàn xác định nếu biết một và một vectơ pháp tuyến của nó.
4. Phương trình tổng quát của đường thẳng
Định nghĩa: Phương trình \(ax + by + c = 0\) với \(a\) và \(b\) không đồng thời bằng \(0\), được gọi là phương trình tổng quát của đường thẳng.
Trường hợp đặc biết:
+ Nếu \(a = 0 => y = \dfrac{-c}{b}; ∆ // Ox\) hoặc trùng Ox (khi c=0)
+ Nếu \(b = 0 => x = \dfrac{-c}{a}; ∆ // Oy\) hoặc trùng Oy (khi c=0)
+ Nếu \(c = 0 => ax + by = 0 => ∆\) đi qua gốc tọa độ
+ Nếu \(∆\) cắt \(Ox\) tại \(A(a; 0)\) và \(Oy\) tại \(B (0; b)\) thì ta có phương trình đoạn chắn của đường thẳng \(∆\) :
\(\dfrac{x}{a} + \dfrac{y}{b} = 1\)
5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng ∆1 và ∆2
có phương trình tổng quát lần lượt là :
a1x+b1y + c1 = 0 và a2x+b2y +c2 = 0
Điểm \(M_0(x_0 ; y_0)\)) là điểm chung của ∆1 và ∆2 khi và chỉ khi \((x_0 ; y_0)\) là nghiệm của hệ hai phương trình:
(1) \(\left\{\begin{matrix} a_{1}x+b_{1}y +c_{1} = 0& \\ a_{2}x+b_{2}y+c_{2}= 0& \end{matrix}\right.\)
Ta có các trường hợp sau:
a) Hệ (1) có một nghiệm: ∆1 cắt ∆2
b) Hệ (1) vô nghiệm: ∆1 // ∆2
c) Hệ (1) có vô số nghiệm: ∆1 \( \equiv \)∆2
6. Góc giữa hai đường thẳng
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành 4 góc.
Nếu ∆1 không vuông góc với ∆2 thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng ∆1 và ∆2.
Nếu ∆1 vuông góc với ∆2 thì ta nói góc giữa ∆1 và ∆2 bằng 900.
Trường hợp ∆1 và ∆2 song song hoặc trùng nhau thì ta quy ước góc giữa ∆1 và ∆2 bằng 00.
Như vậy góc giữa hai đường thẳng luôn bé hơn hoặc bằng 900
Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là \(\widehat{(\Delta _{1},\Delta _{2})}\)
Cho hai đường thẳng:
∆1: a1x+b1y + c1 = 0
∆2: a2x+b2y + c2 = 0
Đặt \(\varphi\) = \(\widehat{(\Delta _{1},\Delta _{2})}\)
\(\cos \varphi\) = \(\dfrac{|a_{1}. A_{2}+b_{1}. B_{2}|}{\sqrt{{a_{1}}^{2}+{b_{1}}^{2}}\sqrt{{a_{2}}^{2}+{b_{2}}^{2}}}\)
Chú ý:
+ \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {n_1} \bot {n_2}\) \(\Leftrightarrow {a_1}.{a_2} + {b_1}.{b_2} = 0\)
+ Nếu \({\Delta _1}\) và \({\Delta _2}\) có phương trình y = k1 x + m1 và y = k2 x + m2 thì
\({\Delta _1} \bot {\Delta _2} \Leftrightarrow {k_1}.{k_2} = - 1\)
7. Công thức tính khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng \(Oxy\) cho đường thẳng \(∆\) có phương trình \(ax+by+c=0\) và điểm \(M_0(x_0 ; y_0)\)).
Khoảng cách từ điểm \(M_0\) đến đường thẳng \(∆\) kí hiệu là \(d(M_0,∆)\), được tính bởi công thức
\(d(M_0,∆)=\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\)
Định nghĩa :
vectơ \(\vec{u}\) được gọi là vectơ chỉ phương của đường thẳng \(∆\) nếu \(\vec{u}\) ≠ \(\vec{0}\) và giá của \(\vec{u}\) song song hoặc trùng với \(∆\)

Nhận xét :
- Nếu \(\vec{u}\) là một vectơ chỉ phương của đường thẳng \(∆\) thì \(k\vec{u} ( k≠ 0)\) cũng là một vectơ chỉ phương của \(∆\) , do đó một đường thẳng có vô số vectơ chỉ phương.
- Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một vectơ chỉ phương của đường thẳng đó.
2. Phương trình tham số của đường thẳng
- Phương trình tham số của đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ; y_0)\) và nhận vectơ \(\vec{u} = (u_1; u_2)\) làm vectơ chỉ phương là :
\(∆\) : \(\left\{\begin{matrix} x= x_{0}+tu_{1}& \\ y= y_{0}+tu_{2}& \end{matrix}\right.\)
-Khi \(u_1≠ 0\) thì tỉ số \(k= \dfrac{u_{2}}{u_{1}}\) được gọi là hệ số góc của đường thẳng.
Từ đây, ta có phương trình đường thẳng \(∆\) đi qua điểm \(M_0(x_0 ; y_0)\) và có hệ số góc k là:
\(y – y_0 = k(x – x_0)\)
Chú ý: Ta đã biết hệ số góc \(k = \tan α\) với góc \(α\) là góc của đường thẳng \(∆\) hợp với chiều dương của trục \(Ox\)
3. Vectơ pháp tuyến của đường thẳng
Định nghĩa: Vectơ \(\vec{n}\) được gọi là vectơ pháp tuyến của đường thẳng \(∆\) nếu \(\vec{n}\) ≠ \(\vec{0}\) và \(\vec{n}\) vuông góc với vectơ chỉ phương của \(∆\)
Nhận xét:
- Nếu \(\vec{n}\) là một vectơ pháp tuyến của đường thẳng \(∆\) thì k\(\vec{n}\) \((k ≠ 0)\) cũng là một vectơ pháp tuyến của \(∆\), do đó một đường thẳng có vô số vec tơ pháp tuyến.
- Một đường thẳng được hoàn toàn xác định nếu biết một và một vectơ pháp tuyến của nó.
4. Phương trình tổng quát của đường thẳng
Định nghĩa: Phương trình \(ax + by + c = 0\) với \(a\) và \(b\) không đồng thời bằng \(0\), được gọi là phương trình tổng quát của đường thẳng.
Trường hợp đặc biết:
+ Nếu \(a = 0 => y = \dfrac{-c}{b}; ∆ // Ox\) hoặc trùng Ox (khi c=0)
+ Nếu \(b = 0 => x = \dfrac{-c}{a}; ∆ // Oy\) hoặc trùng Oy (khi c=0)
+ Nếu \(c = 0 => ax + by = 0 => ∆\) đi qua gốc tọa độ
+ Nếu \(∆\) cắt \(Ox\) tại \(A(a; 0)\) và \(Oy\) tại \(B (0; b)\) thì ta có phương trình đoạn chắn của đường thẳng \(∆\) :
\(\dfrac{x}{a} + \dfrac{y}{b} = 1\)
5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng ∆1 và ∆2
có phương trình tổng quát lần lượt là :
a1x+b1y + c1 = 0 và a2x+b2y +c2 = 0
Điểm \(M_0(x_0 ; y_0)\)) là điểm chung của ∆1 và ∆2 khi và chỉ khi \((x_0 ; y_0)\) là nghiệm của hệ hai phương trình:
(1) \(\left\{\begin{matrix} a_{1}x+b_{1}y +c_{1} = 0& \\ a_{2}x+b_{2}y+c_{2}= 0& \end{matrix}\right.\)
Ta có các trường hợp sau:
a) Hệ (1) có một nghiệm: ∆1 cắt ∆2
b) Hệ (1) vô nghiệm: ∆1 // ∆2
c) Hệ (1) có vô số nghiệm: ∆1 \( \equiv \)∆2
6. Góc giữa hai đường thẳng
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành 4 góc.
Nếu ∆1 không vuông góc với ∆2 thì góc nhọn trong số bốn góc đó được gọi là góc giữa hai đường thẳng ∆1 và ∆2.
Nếu ∆1 vuông góc với ∆2 thì ta nói góc giữa ∆1 và ∆2 bằng 900.
Trường hợp ∆1 và ∆2 song song hoặc trùng nhau thì ta quy ước góc giữa ∆1 và ∆2 bằng 00.
Như vậy góc giữa hai đường thẳng luôn bé hơn hoặc bằng 900
Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là \(\widehat{(\Delta _{1},\Delta _{2})}\)
Cho hai đường thẳng:
∆1: a1x+b1y + c1 = 0
∆2: a2x+b2y + c2 = 0
Đặt \(\varphi\) = \(\widehat{(\Delta _{1},\Delta _{2})}\)
\(\cos \varphi\) = \(\dfrac{|a_{1}. A_{2}+b_{1}. B_{2}|}{\sqrt{{a_{1}}^{2}+{b_{1}}^{2}}\sqrt{{a_{2}}^{2}+{b_{2}}^{2}}}\)
Chú ý:
+ \({\Delta _1} \bot {\Delta _2} \Leftrightarrow {n_1} \bot {n_2}\) \(\Leftrightarrow {a_1}.{a_2} + {b_1}.{b_2} = 0\)
+ Nếu \({\Delta _1}\) và \({\Delta _2}\) có phương trình y = k1 x + m1 và y = k2 x + m2 thì
\({\Delta _1} \bot {\Delta _2} \Leftrightarrow {k_1}.{k_2} = - 1\)
7. Công thức tính khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng \(Oxy\) cho đường thẳng \(∆\) có phương trình \(ax+by+c=0\) và điểm \(M_0(x_0 ; y_0)\)).
Khoảng cách từ điểm \(M_0\) đến đường thẳng \(∆\) kí hiệu là \(d(M_0,∆)\), được tính bởi công thức
\(d(M_0,∆)=\frac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!