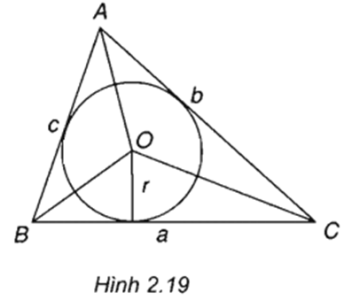
Câu hỏi: Chứng minh công thức S = pr (h. 2.19).

Phương pháp giải
Chi tam giác ABC thành 3 tam giác nhỏ là OAB, OBC, OCA và tính diện tích của chúng.
Lời giải chi tiết

Ta có:
\(\eqalign{
& {S_{OAB}} = {1 \over 2}r. C \cr
& {S_{OAC}} = {1 \over 2}r. B \cr
& {S_{OBC}} = {1 \over 2}r. A \cr
& \Rightarrow {S_{ABC}} = \frac{1}{2}rc + \frac{1}{2}rb + \frac{1}{2}ra\cr &= {1 \over 2}r(a + b + c) = \frac{{a + b + c}}{2}. R\cr &= p. R\cr} \)
(Do \(({{a + b + c} \over 2} = p\) ).
Chi tam giác ABC thành 3 tam giác nhỏ là OAB, OBC, OCA và tính diện tích của chúng.
Lời giải chi tiết
Ta có:
\(\eqalign{
& {S_{OAB}} = {1 \over 2}r. C \cr
& {S_{OAC}} = {1 \over 2}r. B \cr
& {S_{OBC}} = {1 \over 2}r. A \cr
& \Rightarrow {S_{ABC}} = \frac{1}{2}rc + \frac{1}{2}rb + \frac{1}{2}ra\cr &= {1 \over 2}r(a + b + c) = \frac{{a + b + c}}{2}. R\cr &= p. R\cr} \)
(Do \(({{a + b + c} \over 2} = p\) ).