Câu hỏi: Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c' và CH = b'(h. 2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
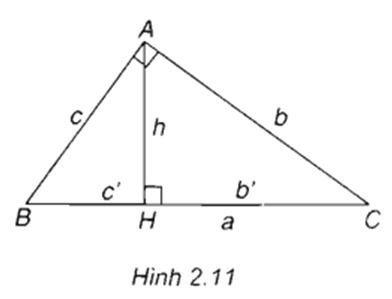
A2 = b2 + (.....) h2 = b' x (.....)
b2 = a x (.....) ah = b x (.....)
c2 = a x (.....)
\(\eqalign{
& {1 \over } = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = { \over a} \cr
& \sin C = \cos B = { \over a} \cr
& \tan B = \cot C = { \over c} \cr
& \cot B = \tan C = { \over b} \cr} \)

A2 = b2 + (.....) h2 = b' x (.....)
b2 = a x (.....) ah = b x (.....)
c2 = a x (.....)
\(\eqalign{
& {1 \over } = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = { \over a} \cr
& \sin C = \cos B = { \over a} \cr
& \tan B = \cot C = { \over c} \cr
& \cot B = \tan C = { \over b} \cr} \)
Lời giải chi tiết
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b' x c'
ah = b x c
\(\eqalign{
& {1 \over {{h^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = {b \over a} \cr
& \sin C = \cos B = {c \over a} \cr
& \tan B = \cot C = {b \over c} \cr
& \cot B = \tan C = {c \over b} \cr} \)
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b' x c'
ah = b x c
\(\eqalign{
& {1 \over {{h^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \cr
& \sin B = \cos C = {b \over a} \cr
& \sin C = \cos B = {c \over a} \cr
& \tan B = \cot C = {b \over c} \cr
& \cot B = \tan C = {c \over b} \cr} \)