Câu hỏi: Trong không gian tọa độ Oxyz, cho các điểm A(4; -1; 2), B(1; 2; 2) và C(1; -1; 5).
Lời giải chi tiết:
Ta có:
\(\eqalign{
& \overrightarrow {AB} = \left({ - 3,3,0} \right),\overrightarrow {AC} = \left({ - 3,0,3} \right),\overrightarrow {BC} = \left({0, - 3,3} \right) \cr
& \Rightarrow AB = \sqrt {{{\left({ - 3} \right)}^2} + {3^2} + {0^2}} = 3\sqrt 2 \cr
& AC = 3\sqrt 2 \cr
& BC = 3\sqrt 2 \cr
& \Rightarrow AB = BC = AC = 3\sqrt 2 . \cr} \)
Vậy tam giác ABC đều.
Lời giải chi tiết:
Ta có:
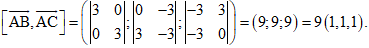
(ABC) đi qua A và nhận \(\overrightarrow n = \left( {1; 1; 1} \right)\) là 1 vectơ pháp tuyến nên (ABC) có phương trình: \(\left( {x - 4} \right) + \left({y + 1} \right) + \left({z - 2} \right) = 0 \Leftrightarrow x + y + z - 5 = 0.\)
Mặt phẳng (ABC) cắt với trục Ox tại điểm A'(5; 0; 0)
Mặt phẳng (ABC) cắt trục Oy tại điểm B'(0; 5; 0)
Mặt phẳng (ABC) cắt trục Oz tại điểm C'(0; 0; 5).
Khi đó khối tứ diện giới hạn bởi mặt phẳng (ABC) và các mặt phẳng tọa độ là tứ diện OA'B'C' và \({V_{OA'B'C'}} = {1 \over 6}OA'. OB'. OC' = {1 \over 6}. 5.5.5 = {{125} \over 6}.\)
Lời giải chi tiết:
Gọi I(a, b, c) là tâm đường tròn ngoại tiếp tam giác ABC ta có:
\(\eqalign{
& \left\{ \matrix{
IA = IB \Leftrightarrow I{A^2} = I{B^2} \Leftrightarrow {\left({a - 4} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 2} \right)^2} = {\left({a - 1} \right)^2} + {\left({b - 2} \right)^2} + {\left({c - 2} \right)^2} \hfill \cr
IA = IC \Leftrightarrow I{A^2} = I{C^2} \Leftrightarrow {\left({a - 4} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 2} \right)^2} = {\left({a - 1} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 5} \right)^2} \hfill \cr
I \in \left({ABC} \right) \Rightarrow a + b + c - 5 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
- 8a + 16 + 2b + 1 = - 2a + 1 - 4b + 4 \hfill \cr
- 8a + 16 + 2b + 1 - 4c + 4 = - 2a + 1 + 2b + 1 - 10c + 25 \hfill \cr
a + b + c - 5 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
6a - 6b = 12 \hfill \cr
6a - 6c = - 6 \hfill \cr
a + b + a = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a - b = 2 \hfill \cr
a - c = - 1 \hfill \cr
a + b + c = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 2 \hfill \cr
b = 0 \hfill \cr
c = 3 \hfill \cr} \right. \Rightarrow I\left({2,0,3} \right). \cr} \)
Trục của đường tròn ngoại tiếp tam giác ABC là đường thẳng đi qua I và vuông góc với (ABC) nên trục đó đi qua I(2; 0; 3) và nhận \(\overrightarrow n = \left( {1,1,1} \right)\) là 1 vectơ chỉ phương.
Do đó trục của đường tròn ngoại tiếp tam giác ABC có phương trình:
\(\left\{ \matrix{
x = 2 + t \hfill \cr
y = t \hfill \cr
z = 3 + t \hfill \cr} \right. \left(\Delta \right)\)
Lời giải chi tiết:
Để ABCD là tứ diện đều thì \(D \in \left( \Delta \right) \Rightarrow D\left({2 + t, t, 3 + t} \right).\)
Và \(DA = AB = 3\sqrt 2 \Leftrightarrow D{A^2} = 18.\)
\(\eqalign{
& \Leftrightarrow {\left({t - 2} \right)^2} + {\left({t + 1} \right)^2} + {\left({t + 1} \right)^2} = 18 \cr
& \Leftrightarrow 3{t^2} = 12 \Leftrightarrow \left[ \matrix{
t = 2 \hfill \cr
t = - 2 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
D\left({4,2,5} \right) \hfill \cr
D\left({0, - 2,1} \right) \hfill \cr} \right.. \cr} \)
Vậy có hai điểm D để ABCD là tứ diện đều là \(D\left( {4,2,5} \right)\) hoặc \(D\left( {0, - 2,1} \right)\).
Câu a
Chứng minh rằng ABC là tam giác đều.Lời giải chi tiết:
Ta có:
\(\eqalign{
& \overrightarrow {AB} = \left({ - 3,3,0} \right),\overrightarrow {AC} = \left({ - 3,0,3} \right),\overrightarrow {BC} = \left({0, - 3,3} \right) \cr
& \Rightarrow AB = \sqrt {{{\left({ - 3} \right)}^2} + {3^2} + {0^2}} = 3\sqrt 2 \cr
& AC = 3\sqrt 2 \cr
& BC = 3\sqrt 2 \cr
& \Rightarrow AB = BC = AC = 3\sqrt 2 . \cr} \)
Vậy tam giác ABC đều.
Câu b
Viết phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.Lời giải chi tiết:
Ta có:
(ABC) đi qua A và nhận \(\overrightarrow n = \left( {1; 1; 1} \right)\) là 1 vectơ pháp tuyến nên (ABC) có phương trình: \(\left( {x - 4} \right) + \left({y + 1} \right) + \left({z - 2} \right) = 0 \Leftrightarrow x + y + z - 5 = 0.\)
Mặt phẳng (ABC) cắt với trục Ox tại điểm A'(5; 0; 0)
Mặt phẳng (ABC) cắt trục Oy tại điểm B'(0; 5; 0)
Mặt phẳng (ABC) cắt trục Oz tại điểm C'(0; 0; 5).
Khi đó khối tứ diện giới hạn bởi mặt phẳng (ABC) và các mặt phẳng tọa độ là tứ diện OA'B'C' và \({V_{OA'B'C'}} = {1 \over 6}OA'. OB'. OC' = {1 \over 6}. 5.5.5 = {{125} \over 6}.\)
Câu c
Viết phương trình trục của đường tròn ngoại tiếp tam giác ABC.Lời giải chi tiết:
Gọi I(a, b, c) là tâm đường tròn ngoại tiếp tam giác ABC ta có:
\(\eqalign{
& \left\{ \matrix{
IA = IB \Leftrightarrow I{A^2} = I{B^2} \Leftrightarrow {\left({a - 4} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 2} \right)^2} = {\left({a - 1} \right)^2} + {\left({b - 2} \right)^2} + {\left({c - 2} \right)^2} \hfill \cr
IA = IC \Leftrightarrow I{A^2} = I{C^2} \Leftrightarrow {\left({a - 4} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 2} \right)^2} = {\left({a - 1} \right)^2} + {\left({b + 1} \right)^2} + {\left({c - 5} \right)^2} \hfill \cr
I \in \left({ABC} \right) \Rightarrow a + b + c - 5 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
- 8a + 16 + 2b + 1 = - 2a + 1 - 4b + 4 \hfill \cr
- 8a + 16 + 2b + 1 - 4c + 4 = - 2a + 1 + 2b + 1 - 10c + 25 \hfill \cr
a + b + c - 5 = 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
6a - 6b = 12 \hfill \cr
6a - 6c = - 6 \hfill \cr
a + b + a = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a - b = 2 \hfill \cr
a - c = - 1 \hfill \cr
a + b + c = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 2 \hfill \cr
b = 0 \hfill \cr
c = 3 \hfill \cr} \right. \Rightarrow I\left({2,0,3} \right). \cr} \)
Trục của đường tròn ngoại tiếp tam giác ABC là đường thẳng đi qua I và vuông góc với (ABC) nên trục đó đi qua I(2; 0; 3) và nhận \(\overrightarrow n = \left( {1,1,1} \right)\) là 1 vectơ chỉ phương.
Do đó trục của đường tròn ngoại tiếp tam giác ABC có phương trình:
\(\left\{ \matrix{
x = 2 + t \hfill \cr
y = t \hfill \cr
z = 3 + t \hfill \cr} \right. \left(\Delta \right)\)
Câu d
Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.Lời giải chi tiết:
Để ABCD là tứ diện đều thì \(D \in \left( \Delta \right) \Rightarrow D\left({2 + t, t, 3 + t} \right).\)
Và \(DA = AB = 3\sqrt 2 \Leftrightarrow D{A^2} = 18.\)
\(\eqalign{
& \Leftrightarrow {\left({t - 2} \right)^2} + {\left({t + 1} \right)^2} + {\left({t + 1} \right)^2} = 18 \cr
& \Leftrightarrow 3{t^2} = 12 \Leftrightarrow \left[ \matrix{
t = 2 \hfill \cr
t = - 2 \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
D\left({4,2,5} \right) \hfill \cr
D\left({0, - 2,1} \right) \hfill \cr} \right.. \cr} \)
Vậy có hai điểm D để ABCD là tứ diện đều là \(D\left( {4,2,5} \right)\) hoặc \(D\left( {0, - 2,1} \right)\).
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!