Câu hỏi: Hình vuông dưới dây có tính chất: mỗi ô ghi một lũy thừa của \(2\); tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau. Hãy điền các số còn thiếu vào các ô trống:


Phương pháp giải
Áp dụng các công thức:
\({x^m}.{x^n} = {x^{m + n}}\)
\({x^m}:{x^n} = {x^{m - n}} \left( {m \ge n} \right)\)
\({a^0} = 1 \left( {a \in {\mathbb N^*}} \right)\)
Lời giải chi tiết
Xét tích các số ở đường chéo ta có:
\({2^7}{.2^4}{.2^1} = {2^{7 + 4 + 1}} = {2^{12}}\)
Theo đề bài mỗi ô ghi một lũy thừa của \(2\); tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau (bằng \({2^{12}}\)).
Xét cột thứ ba ô trống thứ nhất cần điền giá trị là: \({2^{12}}:\left( {{2^6}{{.2}^1}} \right) = {2^{12}}:{2^7} = {2^5}\)
Xét hàng thứ nhất ô trống thứ hai cần điền giá trị là: \({2^{12}}:\left( {{2^7}{{.2}^5}} \right) = {2^{12}}:{2^{12}} = {2^0}\)
Xét hàng thứ hai ô trống thứ nhất cần điền giá trị là: \({2^{12}}:\left( {{2^4}{{.2}^6}} \right) = {2^{12}}:{2^{10}} = {2^2}\)
Xét cột thứ nhất ô trống thứ ba cần điền giá trị là: \({2^{12}}:\left( {{2^7}{{.2}^2}} \right) = {2^{12}}:{2^9} = {2^3}\)
Xét cột thứ hai ô trống thứ ba cần điền giá trị là: \({2^{12}}:\left( {{2^0}{{.2}^4}} \right) = {2^{12}}:{2^4} = {2^8}\)
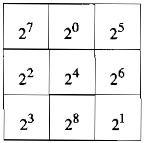
Ta được bảng sau:
Áp dụng các công thức:
\({x^m}.{x^n} = {x^{m + n}}\)
\({x^m}:{x^n} = {x^{m - n}} \left( {m \ge n} \right)\)
\({a^0} = 1 \left( {a \in {\mathbb N^*}} \right)\)
Lời giải chi tiết
Xét tích các số ở đường chéo ta có:
\({2^7}{.2^4}{.2^1} = {2^{7 + 4 + 1}} = {2^{12}}\)
Theo đề bài mỗi ô ghi một lũy thừa của \(2\); tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau (bằng \({2^{12}}\)).
Xét cột thứ ba ô trống thứ nhất cần điền giá trị là: \({2^{12}}:\left( {{2^6}{{.2}^1}} \right) = {2^{12}}:{2^7} = {2^5}\)
Xét hàng thứ nhất ô trống thứ hai cần điền giá trị là: \({2^{12}}:\left( {{2^7}{{.2}^5}} \right) = {2^{12}}:{2^{12}} = {2^0}\)
Xét hàng thứ hai ô trống thứ nhất cần điền giá trị là: \({2^{12}}:\left( {{2^4}{{.2}^6}} \right) = {2^{12}}:{2^{10}} = {2^2}\)
Xét cột thứ nhất ô trống thứ ba cần điền giá trị là: \({2^{12}}:\left( {{2^7}{{.2}^2}} \right) = {2^{12}}:{2^9} = {2^3}\)
Xét cột thứ hai ô trống thứ ba cần điền giá trị là: \({2^{12}}:\left( {{2^0}{{.2}^4}} \right) = {2^{12}}:{2^4} = {2^8}\)
Ta được bảng sau: