Câu hỏi: Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.
Phương pháp giải
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao: \(S=a.h\)
Lời giải chi tiết
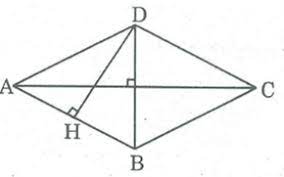
Xét hình thoi \(ABCD.\) Kẻ \(DH ⊥ AB\)
Ta có: \(S_{ABCD}=AB.DH\)
\(∆ AHD\) vuông tại \(H\) \(⇒ DH ≤ AD\)
Suy ra: \(S_{ABCD} \le AB.AD\), mà \(AB = AD\) (gt)
\( \Rightarrow {S_{ABCD}} \le A{B^2}\)
Vậy \(S_{ABCD}\) có giá trị lớn nhất khi bằng \(AB^2\)
Khi đó \(ABCD\) là hình vuông
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.
Diện tích hình thoi bằng tích của cạnh đáy với chiều cao: \(S=a.h\)
Lời giải chi tiết
Xét hình thoi \(ABCD.\) Kẻ \(DH ⊥ AB\)
Ta có: \(S_{ABCD}=AB.DH\)
\(∆ AHD\) vuông tại \(H\) \(⇒ DH ≤ AD\)
Suy ra: \(S_{ABCD} \le AB.AD\), mà \(AB = AD\) (gt)
\( \Rightarrow {S_{ABCD}} \le A{B^2}\)
Vậy \(S_{ABCD}\) có giá trị lớn nhất khi bằng \(AB^2\)
Khi đó \(ABCD\) là hình vuông
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.