Câu hỏi: Điền số hữu tỉ thích hợp vào ô vuông:


Phương pháp giải
Quan sát trên trục số đoạn thẳng đơn vị (chẳng hạn từ điểm \(0\) đến điểm \(1\)) được chia thành \(6\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{6}\) đơn vị cũ.
Lời giải chi tiết
Ta điền vào ô trống như sau:
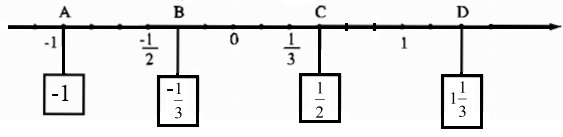
Giải thích:
Quan sát trên trục số đoạn thẳng đơn vị (chẳng hạn từ điểm \(0\) đến điểm \(1\)) được chia thành \(6\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{6}\) đơn vị cũ.
Khi đó:
Điểm \(A\) nằm ở bên trái điểm \(0\) và cách \(0\) một đoạn bằng \(6\) đơn vị mới. Do đó điểm \(A\) biểu diễn số hữu tỉ: \( - \left( {6.\dfrac{1}{6}} \right) = - 1\).
Điểm \(B\) nằm ở bên trái điểm \(0\) và cách \(0\) một đoạn bằng \(2\) đơn vị mới. Do đó điểm \(B\) biểu diễn số hữu tỉ: \( - \left( {2.\dfrac{1}{6}} \right) = \dfrac{-2}{6}= \dfrac{-1}{3}\).
Điểm \(C\) nằm ở bên phải điểm \(0\) và cách điểm \(0\) một đoạn bằng \(3\) đơn vị mới. Do đó điểm \(C\) biểu diễn số hữu tỉ: \(3.\dfrac{1}{6} = \dfrac{3}{6} = \dfrac{1}{2}\).
Điểm \(D\) nằm ở bên phải điểm \(0\) và cách điểm \(0\) một đoạn bằng \(8\) đơn vị mới. Do đó điểm \(D\) biểu diễn số hữu tỉ: \(8.\dfrac{1}{6} = \dfrac{8}{6} = \dfrac{4}{3} = 1\dfrac{1}{3}\).
Quan sát trên trục số đoạn thẳng đơn vị (chẳng hạn từ điểm \(0\) đến điểm \(1\)) được chia thành \(6\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{6}\) đơn vị cũ.
Lời giải chi tiết
Ta điền vào ô trống như sau:
Giải thích:
Quan sát trên trục số đoạn thẳng đơn vị (chẳng hạn từ điểm \(0\) đến điểm \(1\)) được chia thành \(6\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{6}\) đơn vị cũ.
Khi đó:
Điểm \(A\) nằm ở bên trái điểm \(0\) và cách \(0\) một đoạn bằng \(6\) đơn vị mới. Do đó điểm \(A\) biểu diễn số hữu tỉ: \( - \left( {6.\dfrac{1}{6}} \right) = - 1\).
Điểm \(B\) nằm ở bên trái điểm \(0\) và cách \(0\) một đoạn bằng \(2\) đơn vị mới. Do đó điểm \(B\) biểu diễn số hữu tỉ: \( - \left( {2.\dfrac{1}{6}} \right) = \dfrac{-2}{6}= \dfrac{-1}{3}\).
Điểm \(C\) nằm ở bên phải điểm \(0\) và cách điểm \(0\) một đoạn bằng \(3\) đơn vị mới. Do đó điểm \(C\) biểu diễn số hữu tỉ: \(3.\dfrac{1}{6} = \dfrac{3}{6} = \dfrac{1}{2}\).
Điểm \(D\) nằm ở bên phải điểm \(0\) và cách điểm \(0\) một đoạn bằng \(8\) đơn vị mới. Do đó điểm \(D\) biểu diễn số hữu tỉ: \(8.\dfrac{1}{6} = \dfrac{8}{6} = \dfrac{4}{3} = 1\dfrac{1}{3}\).