Câu hỏi: Tính:


Phương pháp giải
\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{{ad}}{{bd}} + \dfrac{{cb}}{{bd}} = \dfrac{{ad + cb}}{{bd}}\)
\(\dfrac{a}{b} - \dfrac{c}{d} =\dfrac{a}{b} + \dfrac{-c}{d}= \dfrac{{ad}}{{bd}} + \dfrac{{-cb}}{{bd}} \)\( = \dfrac{{ad - cb}}{{bd}}\)
\( \dfrac{a}{b} . \dfrac{c}{d} =\dfrac{a.c}{b.d}\)
\( \dfrac{a}{b} : \dfrac{c}{d}=\dfrac{a}{b}.\dfrac{d}{c} = \dfrac{a.d}{b.c}\)
Chú ý: Ta có thể rút gọn các phân số về dạng tối giản rồi thực hiện phép tính.
Lời giải chi tiết
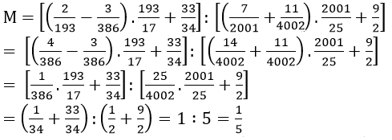
\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{{ad}}{{bd}} + \dfrac{{cb}}{{bd}} = \dfrac{{ad + cb}}{{bd}}\)
\(\dfrac{a}{b} - \dfrac{c}{d} =\dfrac{a}{b} + \dfrac{-c}{d}= \dfrac{{ad}}{{bd}} + \dfrac{{-cb}}{{bd}} \)\( = \dfrac{{ad - cb}}{{bd}}\)
\( \dfrac{a}{b} . \dfrac{c}{d} =\dfrac{a.c}{b.d}\)
\( \dfrac{a}{b} : \dfrac{c}{d}=\dfrac{a}{b}.\dfrac{d}{c} = \dfrac{a.d}{b.c}\)
Chú ý: Ta có thể rút gọn các phân số về dạng tối giản rồi thực hiện phép tính.
Lời giải chi tiết