Câu hỏi: Cho tứ diện \(ABCD\) có \(AD \bot \left( {ABC} \right)\) và \(BD \bot BC\). Khi quay tứ diện đó xung quanh trục là cạnh \(AB\), có bao nhiêu hình nón được tạo thành?
A. Một
B. Hai
C. Ba
D. Bốn
A. Một
B. Hai
C. Ba
D. Bốn
Phương pháp giải
Khi quay tam giác vuông quanh một cạnh góc vuông ta được một hình nón.
Lời giải chi tiết
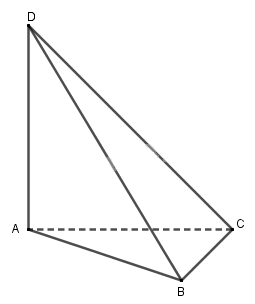
Ta có: \(BC \bot DA, BC \bot BD\) \(\Rightarrow BC \bot \left( {ABD} \right) \Rightarrow BC \bot AB\)
Tam giác \(DAB\) vuông tại \(A\) nên khi quay quanh \(AB\) thì cạnh huyền \(BD\) quét được mặt nón đỉnh \(B\), bán kính đáy \(AD\) và chiều cao \(BA\).
Tam giác \(ABC\) vuông tại \(B\) nên khi quay quanh \(AB\) thì cạnh huyền \(AC\) quét được mặt nón đỉnh \(A\), bán kính đáy \(BC\) và chiều cao \(BA\).
Vậy có hai hình nón được tạo thành.
Khi quay tam giác vuông quanh một cạnh góc vuông ta được một hình nón.
Lời giải chi tiết
Ta có: \(BC \bot DA, BC \bot BD\) \(\Rightarrow BC \bot \left( {ABD} \right) \Rightarrow BC \bot AB\)
Tam giác \(DAB\) vuông tại \(A\) nên khi quay quanh \(AB\) thì cạnh huyền \(BD\) quét được mặt nón đỉnh \(B\), bán kính đáy \(AD\) và chiều cao \(BA\).
Tam giác \(ABC\) vuông tại \(B\) nên khi quay quanh \(AB\) thì cạnh huyền \(AC\) quét được mặt nón đỉnh \(A\), bán kính đáy \(BC\) và chiều cao \(BA\).
Vậy có hai hình nón được tạo thành.
Đáp án B.