Câu hỏi: Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) vẽ một cát tuyến bất kì cắt đường tròn ở \(A\) và \(B.\) Chứng minh rằng tích \(MA.MB\) không đổi.
Phương pháp giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
* Trường hợp \(M\) ở bên trong đường tròn \((O)\)
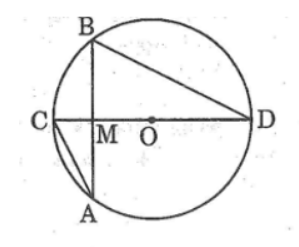
Kẻ cát tuyến \(MAB\) bất kì của \((O)\) và đường thẳng \(MO\) cắt đường tròn \((O)\) tại \(C\) và \(D.\)
Xét hai \(∆MAC\) và \(∆MDB:\)
+) \(\widehat {AMC} = \widehat {BMD}\) (đối đỉnh)
+) \(\widehat {A} = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{BC}\))
Suy ra: \(∆MAC\) đồng dạng \(∆MDB\) \((g.g)\)
\( \Rightarrow \displaystyle {{MA} \over {MD}} = {{MC} \over {MB}}\)
\( \Rightarrow MA.MB = MC.MD\) \((1)\)
Vì \(M, O\) cố định suy ra điểm \(C\) và \(D\) cố định nên độ dài của các đoạn \(MC\) và \(MD\) không đổi, suy ra tích \(MC.MD\) không đổi \((2)\)
Từ \((1)\) và \((2)\) suy ra tích \(MA. MB\) không đổi khi cát tuyến \(MAB\) thay đổi.
* Trường hợp điểm \(M\) ở ngoài đường tròn \((O)\)
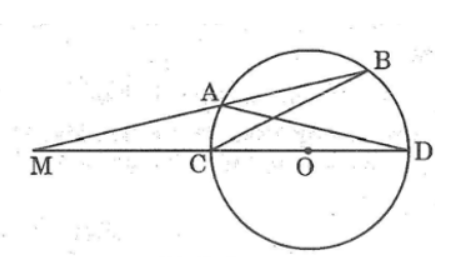
Kẻ cát tuyến \(MAB\) bất kỳ của \((O)\) và đường thẳng \(MO\) cắt đường tròn \((O)\) tại \(C\) và \(D\)
Xét \(∆MAD\) và \(∆MCB:\)
+) \(\widehat M\) chung
+) \(\widehat B = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{AC}\))
Suy ra: \(∆MAD\) đồng dạng \(∆MCB (g.g)\)
\( \Rightarrow \displaystyle {{MC} \over {MA}} = {{MB} \over {MD}} \)
\(\Rightarrow MA.MB = MC.MD\) \( (3)\)
Vì \(M\) và \(O\) cố định suy ra điểm \(C, D\) cố định nên độ dài của các đoạn \(MC\) và \(MD\) không đổi, suy ra tích \(MC. MD\) không đổi \((4)\)
Từ \((3)\) và \((4)\) suy ra tích \(MA. MB\) không đổi khi cát tuyến \(MAB\) thay đổi.
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
* Trường hợp \(M\) ở bên trong đường tròn \((O)\)
Kẻ cát tuyến \(MAB\) bất kì của \((O)\) và đường thẳng \(MO\) cắt đường tròn \((O)\) tại \(C\) và \(D.\)
Xét hai \(∆MAC\) và \(∆MDB:\)
+) \(\widehat {AMC} = \widehat {BMD}\) (đối đỉnh)
+) \(\widehat {A} = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{BC}\))
Suy ra: \(∆MAC\) đồng dạng \(∆MDB\) \((g.g)\)
\( \Rightarrow \displaystyle {{MA} \over {MD}} = {{MC} \over {MB}}\)
\( \Rightarrow MA.MB = MC.MD\) \((1)\)
Vì \(M, O\) cố định suy ra điểm \(C\) và \(D\) cố định nên độ dài của các đoạn \(MC\) và \(MD\) không đổi, suy ra tích \(MC.MD\) không đổi \((2)\)
Từ \((1)\) và \((2)\) suy ra tích \(MA. MB\) không đổi khi cát tuyến \(MAB\) thay đổi.
* Trường hợp điểm \(M\) ở ngoài đường tròn \((O)\)
Kẻ cát tuyến \(MAB\) bất kỳ của \((O)\) và đường thẳng \(MO\) cắt đường tròn \((O)\) tại \(C\) và \(D\)
Xét \(∆MAD\) và \(∆MCB:\)
+) \(\widehat M\) chung
+) \(\widehat B = \widehat D\) (hai góc nội tiếp cùng chắn cung \(\overparen{AC}\))
Suy ra: \(∆MAD\) đồng dạng \(∆MCB (g.g)\)
\( \Rightarrow \displaystyle {{MC} \over {MA}} = {{MB} \over {MD}} \)
\(\Rightarrow MA.MB = MC.MD\) \( (3)\)
Vì \(M\) và \(O\) cố định suy ra điểm \(C, D\) cố định nên độ dài của các đoạn \(MC\) và \(MD\) không đổi, suy ra tích \(MC. MD\) không đổi \((4)\)
Từ \((3)\) và \((4)\) suy ra tích \(MA. MB\) không đổi khi cát tuyến \(MAB\) thay đổi.