Câu hỏi: Điền các số hữu tỉ thích hợp vào các ô trống trong hình tháp dưới đây.


Phương pháp giải
\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{{ad}}{{bd}} + \dfrac{{cb}}{{bd}} = \dfrac{{ad + cb}}{{bd}}\)
\(\dfrac{a}{b} - \dfrac{c}{d} =\dfrac{a}{b} + \dfrac{-c}{d}= \dfrac{{ad}}{{bd}} + \dfrac{{-cb}}{{bd}} \)\( = \dfrac{{ad - cb}}{{bd}}\)
Lời giải chi tiết
\(\dfrac{1}{4} - \dfrac{1}{6} = \dfrac{3}{{12}} - \dfrac{2}{{12}} = \dfrac{{3 - 2}}{{12}} = \dfrac{1}{{12}}\)
\(\dfrac{1}{6} + \dfrac{{ - 1}}{4} = \dfrac{2}{{12}} + \dfrac{{ - 3}}{{12}} = \dfrac{{2 + \left( { - 3} \right)}}{{12}} \)\( = \dfrac{{ - 1}}{{12}}\)
\(\dfrac{1}{{12}} - \left( {\dfrac{{ - 1}}{4}} \right) = \dfrac{1}{{12}} + \dfrac{1}{4}\)\( = \dfrac{1}{{12}} + \dfrac{3}{{12}} = \dfrac{{1 + 3}}{{12}} = \dfrac{4}{{12}} = \dfrac{1}{3}\)
Ta điền được các số sau:
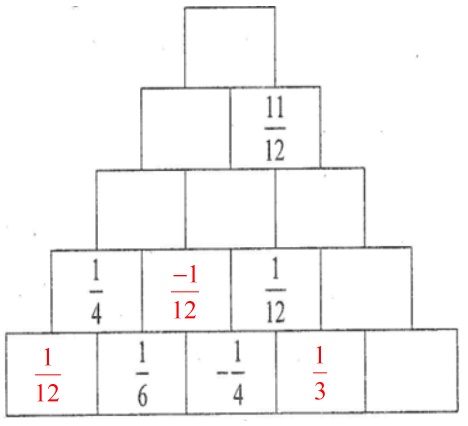
\(\dfrac{1}{4} + \dfrac{{ - 1}}{{12}} = \dfrac{3}{{12}} + \dfrac{{ - 1}}{{12}} \)\( = \dfrac{{3 + \left( { - 1} \right)}}{{12}} = \dfrac{2}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{ - 1}}{{12}} + \dfrac{1}{{12}} = 0\)
Ta điền tiếp được các số sau:
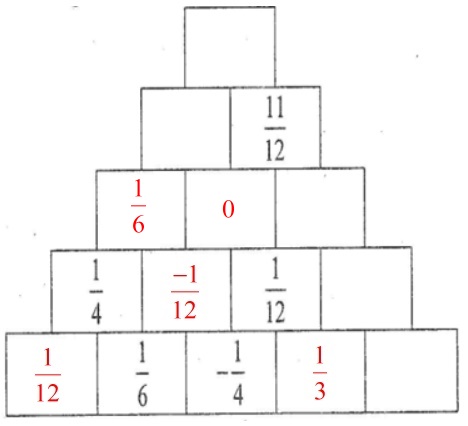
\(\dfrac{1}{6} + 0 = \dfrac{1}{6}\)
\(\dfrac{1}{6} + \dfrac{{11}}{{12}} = \dfrac{2}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{2 + 11}}{{12}} \)\( = \dfrac{{13}}{{12}}\)
Ta điền tiếp được các số sau:
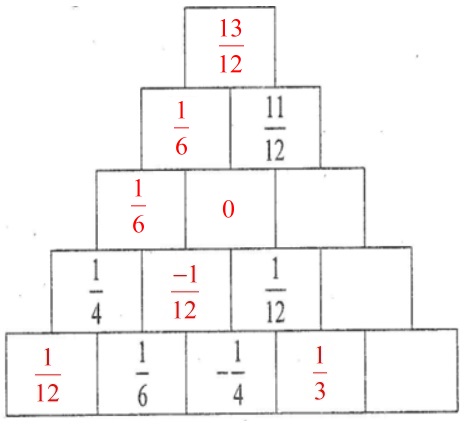
\(\begin{array}{l}
\dfrac{{11}}{{12}} - 0 = \dfrac{{11}}{{12}}\\
\dfrac{{11}}{{12}} - \dfrac{1}{{12}} = \dfrac{{11 - 1}}{{12}} = \dfrac{{10}}{{12}} = \dfrac{5}{6}\\
\dfrac{5}{6} - \dfrac{1}{3} = \dfrac{5}{6} - \dfrac{2}{6} = \dfrac{{5 - 2}}{6} = \dfrac{3}{6} = \dfrac{1}{2}
\end{array}\)
Ta điền được các số còn lại như sau:
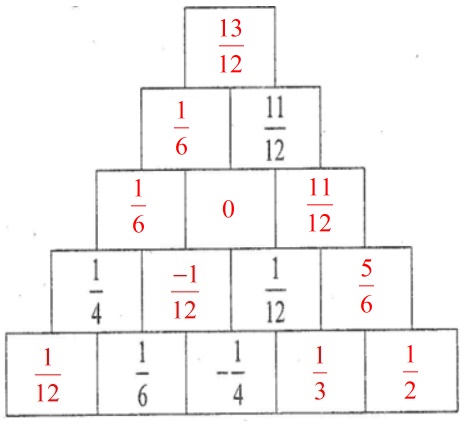
\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{{ad}}{{bd}} + \dfrac{{cb}}{{bd}} = \dfrac{{ad + cb}}{{bd}}\)
\(\dfrac{a}{b} - \dfrac{c}{d} =\dfrac{a}{b} + \dfrac{-c}{d}= \dfrac{{ad}}{{bd}} + \dfrac{{-cb}}{{bd}} \)\( = \dfrac{{ad - cb}}{{bd}}\)
Lời giải chi tiết
\(\dfrac{1}{4} - \dfrac{1}{6} = \dfrac{3}{{12}} - \dfrac{2}{{12}} = \dfrac{{3 - 2}}{{12}} = \dfrac{1}{{12}}\)
\(\dfrac{1}{6} + \dfrac{{ - 1}}{4} = \dfrac{2}{{12}} + \dfrac{{ - 3}}{{12}} = \dfrac{{2 + \left( { - 3} \right)}}{{12}} \)\( = \dfrac{{ - 1}}{{12}}\)
\(\dfrac{1}{{12}} - \left( {\dfrac{{ - 1}}{4}} \right) = \dfrac{1}{{12}} + \dfrac{1}{4}\)\( = \dfrac{1}{{12}} + \dfrac{3}{{12}} = \dfrac{{1 + 3}}{{12}} = \dfrac{4}{{12}} = \dfrac{1}{3}\)
Ta điền được các số sau:
\(\dfrac{1}{4} + \dfrac{{ - 1}}{{12}} = \dfrac{3}{{12}} + \dfrac{{ - 1}}{{12}} \)\( = \dfrac{{3 + \left( { - 1} \right)}}{{12}} = \dfrac{2}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{ - 1}}{{12}} + \dfrac{1}{{12}} = 0\)
Ta điền tiếp được các số sau:
\(\dfrac{1}{6} + 0 = \dfrac{1}{6}\)
\(\dfrac{1}{6} + \dfrac{{11}}{{12}} = \dfrac{2}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{2 + 11}}{{12}} \)\( = \dfrac{{13}}{{12}}\)
Ta điền tiếp được các số sau:
\(\begin{array}{l}
\dfrac{{11}}{{12}} - 0 = \dfrac{{11}}{{12}}\\
\dfrac{{11}}{{12}} - \dfrac{1}{{12}} = \dfrac{{11 - 1}}{{12}} = \dfrac{{10}}{{12}} = \dfrac{5}{6}\\
\dfrac{5}{6} - \dfrac{1}{3} = \dfrac{5}{6} - \dfrac{2}{6} = \dfrac{{5 - 2}}{6} = \dfrac{3}{6} = \dfrac{1}{2}
\end{array}\)
Ta điền được các số còn lại như sau: