Câu hỏi: Tìm hai số có hiệu là \(13\) sao cho tích của chúng là bé nhất.
A. \(13\) và \(0\)
B. \(\dfrac{{13}}{2}\) và \(- \dfrac{{13}}{2}\)
C. \(15\) và \(2\)
D. \(30\) và \(15\)
A. \(13\) và \(0\)
B. \(\dfrac{{13}}{2}\) và \(- \dfrac{{13}}{2}\)
C. \(15\) và \(2\)
D. \(30\) và \(15\)
Phương pháp giải
- Lập hàm số tính tích của hai số.
- Tìm GTNN của hàm số trên và suy ra kết luận.
Lời giải chi tiết
Gọi số thứ nhất là \(x\) và số thứ hai là \(x - 13\).
Tích hai số là \(P\left( x \right) = x\left({x - 13} \right) = {x^2} - 13x\).
Có \(P'\left( x \right) = 2x - 13 = 0 \Leftrightarrow x = \dfrac{{13}}{2}\).
Bảng biến thiên:
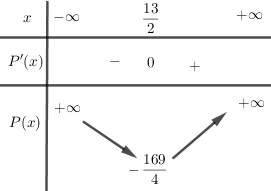
Do đó \(\mathop {\min }\limits_\mathbb{R} P\left( x \right) = - \dfrac{{169}}{4}\) khi \(x = \dfrac{{13}}{2}\).
Vậy hai số đó là \(\dfrac{{13}}{2}\) và \(- \dfrac{{13}}{2}\).
Cách khác:
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích p(x) = x(x + 13) = x2 + 13x;
p'(x) = 2x + 13; p'(x) = 0 ⇔ x = -13/2.
Bảng biến thiên
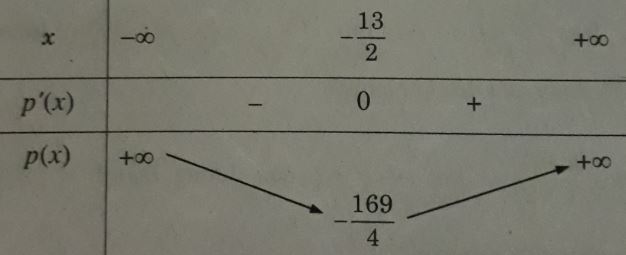
Vậy tích hai số là bé nhất khi một số là x = -13/2 và số kia là x + 13 = 13/2.
- Lập hàm số tính tích của hai số.
- Tìm GTNN của hàm số trên và suy ra kết luận.
Lời giải chi tiết
Gọi số thứ nhất là \(x\) và số thứ hai là \(x - 13\).
Tích hai số là \(P\left( x \right) = x\left({x - 13} \right) = {x^2} - 13x\).
Có \(P'\left( x \right) = 2x - 13 = 0 \Leftrightarrow x = \dfrac{{13}}{2}\).
Bảng biến thiên:
Do đó \(\mathop {\min }\limits_\mathbb{R} P\left( x \right) = - \dfrac{{169}}{4}\) khi \(x = \dfrac{{13}}{2}\).
Vậy hai số đó là \(\dfrac{{13}}{2}\) và \(- \dfrac{{13}}{2}\).
Cách khác:
Gọi một trong hai số phải tìm là x, ta có số kia là x + 13
Xét tích p(x) = x(x + 13) = x2 + 13x;
p'(x) = 2x + 13; p'(x) = 0 ⇔ x = -13/2.
Bảng biến thiên
Vậy tích hai số là bé nhất khi một số là x = -13/2 và số kia là x + 13 = 13/2.
Đáp án B.