Câu hỏi: Trong thí nghiệm Y-âng về giao thoa ánh sáng, màn quan sát E cách mặt phẳng chứa hai khe 1 2 SSmột khoảng 1,2m. Đặt giữa mặt phẳng hai khe một thấu kính hội tụ, người ta tìm được 2 vị trí của thấu kính cách nhau 72cm cho ảnh rõ nét của hai khe trên màn, ở vị trí ảnh lớn hơn thì khoảng cách giữa hai khe ảnh là 4mm. Bỏ thấu kính đi, rồi chiếu sáng hai khe bằng nguồn điểm S phát bức xạ đơn sắc 750nm thì khoảng vân thu được trên màn là
A. 3,6 mm.
B. 0,225 mm.
C. 1,25 mm.
D. 0,9 mm.
A. 3,6 mm.
B. 0,225 mm.
C. 1,25 mm.
D. 0,9 mm.
Phương pháp:
+ Sử dụng công thức thấu kính: $\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{{{d}^{\prime }}}$
+ Sử dụng công thức viét: $\left\{ \begin{array}{*{35}{l}}
{{x}_{1}}+{{x}_{2}}=S \\
{{x}_{1}}\cdot {{x}_{2}}=P \\
\end{array}\Rightarrow {{X}^{2}}-SX+P=0 \right.$
+ Sử dụng công thức tính khoảng vân: $i=\dfrac{\lambda D}{a}$
Cách giải:
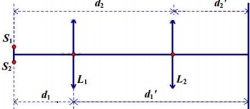
Trên hình vẽ, ta có ${{L}_{1}};{{L}_{2}}$ là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi f là tiêu ực của thấu kính, ta có:
+ Xét vị trí ${{L}_{1}}:\dfrac{1}{f}=\dfrac{1}{{{d}_{1}}}+\dfrac{1}{d_{1}^{\prime }}$
+ Xét vị trí ${{L}_{2}}:\dfrac{1}{f}=\dfrac{1}{{{d}_{2}}}+\dfrac{1}{d_{2}^{\prime }}\Rightarrow \dfrac{1}{{{d}_{1}}}+\dfrac{1}{d_{1}^{\prime }}=\dfrac{1}{{{d}_{2}}}+\dfrac{1}{d_{2}^{\prime }}$
Lại có: ${{d}_{1}}+d_{1}^{\prime }={{d}_{2}}+{{d}_{2}}^{\prime }=S\Rightarrow {{d}_{1}}\cdot d_{1}^{\prime }={{d}_{2}}{{d}_{2}}^{\prime }=P$ (1)
Từ (1) ta suy ra ${{d}_{1}};{{d}_{1}}^{\prime }$ là 2 nghiệm của phương trình: ${{X}^{2}}-S\text{X}+P=0$ và ${{d}_{2}};{{d}_{2}}'$ cũng vậy.
Phương trình trên là phương trình bậc 2 chó 2 nghiệm phân biệt ${{X}_{1}},{{X}_{2}}$
Do ${{d}_{1}}\ne {{d}_{2}}$ nên ${{X}_{1}}={{d}_{1}}=d_{2}^{\prime }\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{ }{{X}_{2}}={{d}_{2}}=d_{1}^{\prime }$
Theo đề bài ta có: $\left\{ \begin{array}{*{35}{l}}
{{d}_{1}}+d_{1}^{\prime }=1,2m=120\text{cm} \\
{{d}_{2}}-{{d}_{1}}=d_{1}^{\prime }-{{d}_{1}}=72\text{cm} \\
\end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}}
{{d}_{1}}=d_{2}^{\prime }=24~\text{cm} \\
d_{1}^{\prime }={{d}_{2}}=96~\text{cm} \\
\end{array} \right. \right.$
Ta xét 1 vị trí bất kì của thấu kính
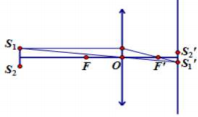
Từ hình vẽ, ta có: $S_{1}^{\prime }S_{2}^{\prime }={{S}_{1}}{{S}_{2}}\dfrac{{{d}^{\prime }}}{d}$
Suy ra để có ảnh lớn hơn, ta phải có $\dfrac{{{d}^{\prime }}}{d}>1$. Tức là thấu kính gần ${{S}_{1}}{{S}_{2}}$ hơn
Khi đó: $\left\{ \begin{array}{*{35}{l}}
d=24~\text{cm} \\
{{d}^{\prime }}=96~\text{cm} \\
\end{array}\Rightarrow {{S}_{1}}{{S}_{2}}={{S}_{1}}~\text{S}_{2}^{\prime }\dfrac{d}{{{d}^{\prime }}}=4\dfrac{24}{96}=1~\text{mm} \right.$
Vậy $a=1~\text{mm}$
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
$i=\dfrac{\lambda D}{a}=\dfrac{750\cdot {{10}^{-9}}\cdot 1,2}{{{10}^{-3}}}={{9.10}^{-4}}~\text{m}=0,9~\text{mm}$
+ Sử dụng công thức thấu kính: $\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{{{d}^{\prime }}}$
+ Sử dụng công thức viét: $\left\{ \begin{array}{*{35}{l}}
{{x}_{1}}+{{x}_{2}}=S \\
{{x}_{1}}\cdot {{x}_{2}}=P \\
\end{array}\Rightarrow {{X}^{2}}-SX+P=0 \right.$
+ Sử dụng công thức tính khoảng vân: $i=\dfrac{\lambda D}{a}$
Cách giải:
Trên hình vẽ, ta có ${{L}_{1}};{{L}_{2}}$ là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi f là tiêu ực của thấu kính, ta có:
+ Xét vị trí ${{L}_{1}}:\dfrac{1}{f}=\dfrac{1}{{{d}_{1}}}+\dfrac{1}{d_{1}^{\prime }}$
+ Xét vị trí ${{L}_{2}}:\dfrac{1}{f}=\dfrac{1}{{{d}_{2}}}+\dfrac{1}{d_{2}^{\prime }}\Rightarrow \dfrac{1}{{{d}_{1}}}+\dfrac{1}{d_{1}^{\prime }}=\dfrac{1}{{{d}_{2}}}+\dfrac{1}{d_{2}^{\prime }}$
Lại có: ${{d}_{1}}+d_{1}^{\prime }={{d}_{2}}+{{d}_{2}}^{\prime }=S\Rightarrow {{d}_{1}}\cdot d_{1}^{\prime }={{d}_{2}}{{d}_{2}}^{\prime }=P$ (1)
Từ (1) ta suy ra ${{d}_{1}};{{d}_{1}}^{\prime }$ là 2 nghiệm của phương trình: ${{X}^{2}}-S\text{X}+P=0$ và ${{d}_{2}};{{d}_{2}}'$ cũng vậy.
Phương trình trên là phương trình bậc 2 chó 2 nghiệm phân biệt ${{X}_{1}},{{X}_{2}}$
Do ${{d}_{1}}\ne {{d}_{2}}$ nên ${{X}_{1}}={{d}_{1}}=d_{2}^{\prime }\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{ }{{X}_{2}}={{d}_{2}}=d_{1}^{\prime }$
Theo đề bài ta có: $\left\{ \begin{array}{*{35}{l}}
{{d}_{1}}+d_{1}^{\prime }=1,2m=120\text{cm} \\
{{d}_{2}}-{{d}_{1}}=d_{1}^{\prime }-{{d}_{1}}=72\text{cm} \\
\end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}}
{{d}_{1}}=d_{2}^{\prime }=24~\text{cm} \\
d_{1}^{\prime }={{d}_{2}}=96~\text{cm} \\
\end{array} \right. \right.$
Ta xét 1 vị trí bất kì của thấu kính
Từ hình vẽ, ta có: $S_{1}^{\prime }S_{2}^{\prime }={{S}_{1}}{{S}_{2}}\dfrac{{{d}^{\prime }}}{d}$
Suy ra để có ảnh lớn hơn, ta phải có $\dfrac{{{d}^{\prime }}}{d}>1$. Tức là thấu kính gần ${{S}_{1}}{{S}_{2}}$ hơn
Khi đó: $\left\{ \begin{array}{*{35}{l}}
d=24~\text{cm} \\
{{d}^{\prime }}=96~\text{cm} \\
\end{array}\Rightarrow {{S}_{1}}{{S}_{2}}={{S}_{1}}~\text{S}_{2}^{\prime }\dfrac{d}{{{d}^{\prime }}}=4\dfrac{24}{96}=1~\text{mm} \right.$
Vậy $a=1~\text{mm}$
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
$i=\dfrac{\lambda D}{a}=\dfrac{750\cdot {{10}^{-9}}\cdot 1,2}{{{10}^{-3}}}={{9.10}^{-4}}~\text{m}=0,9~\text{mm}$
Đáp án D.