GS.Xoăn
Trần Văn Quân
Mùa thi Đại học 2014 vừa trôi qua, năm học 2014-2015 đã đến. Vì một lí do nào đó mà dạo này diễn đàn vắng bóng thành viên nên mình lập topic này để ôn tập và nâng cao kiến thức để ôn thi đại học 2015. Mong mọi người ủng hộ topic để diễn đàn ngày một càng sôi nổi, là nơi giao lưu, chia sẻ và trao đổi kiến thức.;)
Quy định post bài trong topic:
+ Post bài theo đúng thứ tự bài 1, bài 2,..., Không spam không chém gió =;
+Hạn chế trùng lặp các dạng bài toán, những bài toán quá dễ hay quá khó. Những bài toán hay có thể post lại và ghi rõ nguồn
+Lời giải cần rõ ràng dễ hiểu. Khuyến khích những lời giải nhanh phù hợp với câu hỏi trắc nghiệm
+Không post quá nhiều bài toán khi những bài toán trước chưa có lời giải
+Hy vọng có những bài toán sáng tạo :D
P/s: Những bạn nào biết thêm latex mình sẽ đưa link tổng hợp cho topic để làm nguồn tài liệu ôn thi
Bài toán mở đầu:
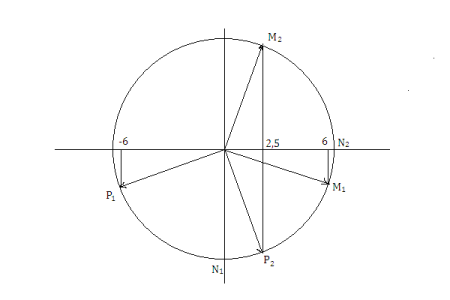
Bài toán 1: Sóng ngang có chu kỳ $T$, bước sóng $\lambda$, lan truyền trên mặt nước với biên độ không đổi. Xét trên một phương truyền sóng, sóng truyền từ điểm M rồi mới đến điểm N cách nó $\dfrac{\lambda }{5}$. Nếu tại thời điểm t, điểm M qua vị trí cân bằng và đang đi lên thì sau khoảng thời gian ngắn nhất bao nhiêu thì điểm N sẽ hạ xuống thấp nhất?
A. 11T/20
B. 19T/20
C. T/20
D. 9T/20
Quy định post bài trong topic:
+ Post bài theo đúng thứ tự bài 1, bài 2,..., Không spam không chém gió =;
+Hạn chế trùng lặp các dạng bài toán, những bài toán quá dễ hay quá khó. Những bài toán hay có thể post lại và ghi rõ nguồn
+Lời giải cần rõ ràng dễ hiểu. Khuyến khích những lời giải nhanh phù hợp với câu hỏi trắc nghiệm
+Không post quá nhiều bài toán khi những bài toán trước chưa có lời giải
+Hy vọng có những bài toán sáng tạo :D
P/s: Những bạn nào biết thêm latex mình sẽ đưa link tổng hợp cho topic để làm nguồn tài liệu ôn thi
Bài toán mở đầu:
Bài toán 1: Sóng ngang có chu kỳ $T$, bước sóng $\lambda$, lan truyền trên mặt nước với biên độ không đổi. Xét trên một phương truyền sóng, sóng truyền từ điểm M rồi mới đến điểm N cách nó $\dfrac{\lambda }{5}$. Nếu tại thời điểm t, điểm M qua vị trí cân bằng và đang đi lên thì sau khoảng thời gian ngắn nhất bao nhiêu thì điểm N sẽ hạ xuống thấp nhất?
A. 11T/20
B. 19T/20
C. T/20
D. 9T/20
Last edited: