t.t.phuong
New Member
Bài toán
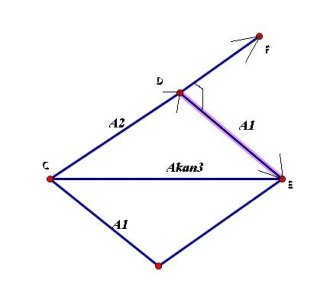
Một chất điểm tham gia đồng thời hai dao động trên trục $Ox$ có phương trình $x_1=A_1\cos 10t$ , $x_2=A_2 \cos (10t + \varphi_2 )$. Phương trình dao động tổng hợp là $x=A_1\sqrt{3} \cos (10t+ \varphi )$ , trong đó $\varphi_2 - \varphi =\dfrac{\pi}{6}$. Tính tỉ số $\dfrac{\varphi}{\varphi_2}$
A. $\dfrac{2}{3}$ hoặc $\dfrac{4}{3}$
B. $\dfrac{1}{3}$ hoặc $\dfrac{2}{3}$
C. $\dfrac{1}{2}$ hoặc $\dfrac{3}{4}$
D. $\dfrac{3}{4}$ hoặc $\dfrac{2}{5}$

Một chất điểm tham gia đồng thời hai dao động trên trục $Ox$ có phương trình $x_1=A_1\cos 10t$ , $x_2=A_2 \cos (10t + \varphi_2 )$. Phương trình dao động tổng hợp là $x=A_1\sqrt{3} \cos (10t+ \varphi )$ , trong đó $\varphi_2 - \varphi =\dfrac{\pi}{6}$. Tính tỉ số $\dfrac{\varphi}{\varphi_2}$
A. $\dfrac{2}{3}$ hoặc $\dfrac{4}{3}$
B. $\dfrac{1}{3}$ hoặc $\dfrac{2}{3}$
C. $\dfrac{1}{2}$ hoặc $\dfrac{3}{4}$
D. $\dfrac{3}{4}$ hoặc $\dfrac{2}{5}$
m.n lm jup mk bai nay na
1 chat diem tham ja dong thoi 2 dao dong tren truc Ox co phuong trinh x1= A1\cos 10t ; x2 = A2\cos (10t + phi2). phuong trinh dao dong tong hop x = A1 can3\cos (10t + phi), trong do phi2 - phi = pi/6. tir so phi/ phi2 =?
A. 2/3 hoac 4/3
B. 1/3 hoac 2/3
C. 1/2 hoac 3/4
D. 3/4 hoac 2/5

Lần chỉnh sửa cuối bởi 1 quản trị viên: