Câu hỏi: Một con lắc lò xo treo thẳng đứng gồm vật nặng có khối lượng m = 100g và lò xo khối lượng không đáng kể. Chọn gốc toạ độ ở vị trí cân bằng, chiều dương hướng lên. Biết con lắc lò xo dao động điều hoà theo phương trình: $x=4\cos \left( 10t-\dfrac{\pi }{3} \right)(cm)$. Lấy $g=10~\text{m}/{{\text{s}}^{2}}.$ Độ lớn lực đàn hồi tác dụng vào vật tại thời điểm vật đã đi quãng đường S = 10cm kể từ lúc t = 0 bằng bao nhiêu?
A. 1,4 N.
B. 0,9 N.
C. 1,2 N.
D. 0,6 N.
A. 1,4 N.
B. 0,9 N.
C. 1,2 N.
D. 0,6 N.
Phương pháp:
Độ lớn lực đàn hồi: ${{F}_{dh}}=k\cdot \left( l-{{l}_{0}} \right)=k\cdot \Delta l$
Độ biến dạng tại VTCB: $\Delta l=\dfrac{mg}{k}$
Tần số góc: $\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{g}{\Delta l}}$
Cách giải:
Phương trình dao động: $x=4\cos \left( 10t-\dfrac{\pi }{3} \right)(\text{cm})\Rightarrow \left\{ \begin{array}{*{35}{l}}
A=4~\text{cm}=0,04~\text{m} \\
\omega =10\text{rad}/\text{s} \\
\end{array} \right.$
Độ cứng của lò xo: $k=m\cdot {{\omega }^{2}}=0,{{1.10}^{2}}=10~\text{N}/\text{m}$
Độ giãn của lò xo tại VTCB: $\Delta l=\dfrac{g}{{{\omega }^{2}}}=\dfrac{10}{{{10}^{2}}}=0,1~\text{m}=10~\text{cm}$
Tại t = 0 vật có $x=2~\text{cm}$ và chuyển động theo chiều dương.
Chú ý là chiều dương hướng lên.
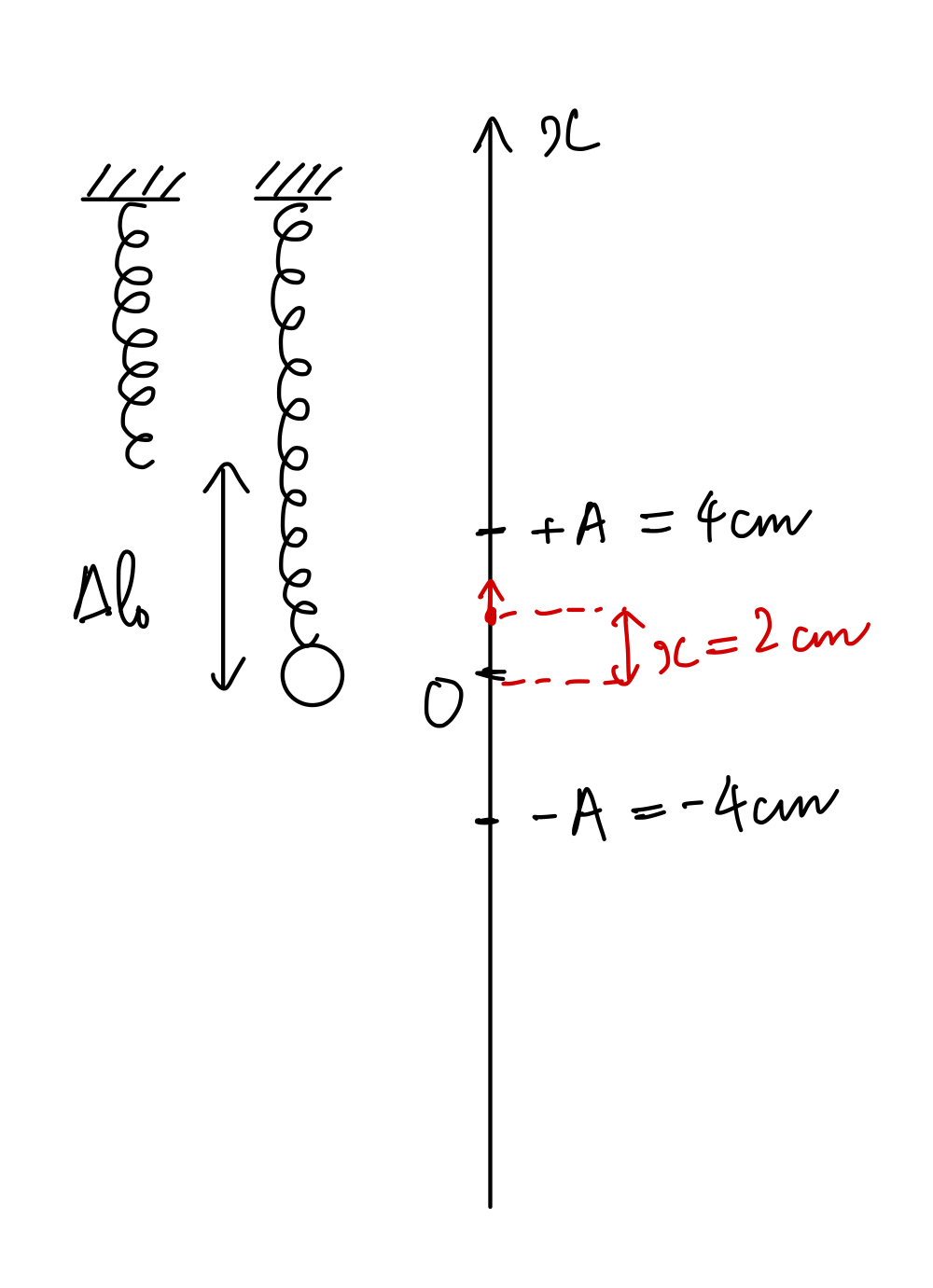
Khi đó để đi được 10 cm thì vật sẽ đi lên đến biên dương (mất 2 cm) và đi từ biên dương xuống đến biên âm (mất 8 cm).
Độ lớn lực đàn hồi tác dụng vào vật tại thời điểm đó là:
${{F}_{dh}}=k\cdot (\Delta l+A)=10.(0,1+0,04)=1,4N$
Độ lớn lực đàn hồi: ${{F}_{dh}}=k\cdot \left( l-{{l}_{0}} \right)=k\cdot \Delta l$
Độ biến dạng tại VTCB: $\Delta l=\dfrac{mg}{k}$
Tần số góc: $\omega =\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{g}{\Delta l}}$
Cách giải:
Phương trình dao động: $x=4\cos \left( 10t-\dfrac{\pi }{3} \right)(\text{cm})\Rightarrow \left\{ \begin{array}{*{35}{l}}
A=4~\text{cm}=0,04~\text{m} \\
\omega =10\text{rad}/\text{s} \\
\end{array} \right.$
Độ cứng của lò xo: $k=m\cdot {{\omega }^{2}}=0,{{1.10}^{2}}=10~\text{N}/\text{m}$
Độ giãn của lò xo tại VTCB: $\Delta l=\dfrac{g}{{{\omega }^{2}}}=\dfrac{10}{{{10}^{2}}}=0,1~\text{m}=10~\text{cm}$
Tại t = 0 vật có $x=2~\text{cm}$ và chuyển động theo chiều dương.
Chú ý là chiều dương hướng lên.
Khi đó để đi được 10 cm thì vật sẽ đi lên đến biên dương (mất 2 cm) và đi từ biên dương xuống đến biên âm (mất 8 cm).
Độ lớn lực đàn hồi tác dụng vào vật tại thời điểm đó là:
${{F}_{dh}}=k\cdot (\Delta l+A)=10.(0,1+0,04)=1,4N$
Đáp án A.