Lý thuyết hàm số lũy thừa

Câu hỏi: 1. Khái niệm hàm số lũy thừa
Hàm số lũy thừa là các hàm số dạng $y = {x^\alpha }\left( {\alpha \in R} \right)$. Các hàm số lũy thừa có tập xác định khác nhau, tùy theo $\alpha$ :
- Nếu $\alpha$ nguyên dương thì tập các định là $R$.
- Nếu $\alpha $ nguyên âm hoặc $\alpha = 0$ thì tập các định là $R\backslash \left\{ 0 \right\}$.
- Nếu $\alpha $ không nguyên thì tập các định là $\left( {0; + \infty } \right)$.
Chú ý: Hàm số $y = \sqrt x $ có tập xác định là $\left[ {0; + \infty } \right)$, hàm số $y = \sqrt[3]{x}$ có tập xác định $R$, trong khi đó các hàm $y = {x^{\dfrac{1}{2}}},y = {x^{\dfrac{1}{3}}}$ đều có tập xác định $\left(0; +∞\right)$. Vì vậy $y = \sqrt x $ và $y = {x^{\dfrac{1}{2}}}$ ( hay $y = \sqrt[3]{x}$ và $y = {x^{\dfrac{1}{3}}}$ ) là những hàm số khác nhau.
2. Đạo hàm của hàm số lũy thừa với số mũ tổng quát
- Hàm số $y = {x^\alpha }$ có đạo hàm tai mọi $x ∈ \left(0; +∞\right)$ và $y' = \left( {{x^\alpha }} \right)' = \alpha {x^{\alpha - 1}}$
- Nếu hàm số $u=u\left(x\right)$ nhận giá trị dương và có đạo hàm trong khoảng $J$ thì hàm số $y = {u^\alpha }\left( x \right)$ cũng có đạo hàm trên $J$ và $y' = \left[ {{u^\alpha }\left( x \right)} \right]' = \alpha {u^{\alpha - 1}}\left( x \right)u'\left( x \right)$
3. Đạo hàm của hàm số lũy thừa với số mũ nguyên dương
Trong trường hợp số mũ nguyên dương, hàm số lũy thừa $y=x^n$ có tập xác định là $R$ và có đạo hàm trên toàn trục số. Công thức tính đạo hàm số lũy thừa tổng quát được mở rộng thành $\forall x \in R,\left( {{x^n}} \right)' = n{x^{n - 1}}$ và $\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)$ nếu $u= u\left(x\right) $ có đạo hàm trong khoảng $J$.
4. Đạo hàm của hàm số lũy thừa với số mũ nguyên âm
Nếu số mũ là số nguyên âm thì hàm số lũy thừa $y=x^n$ có tập xác định là $R\backslash \left\{ 0 \right\}$ và có đạo hàm tại mọi $x$ khác $0$, công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành $\forall x \ne 0,\left( {{x^n}} \right)' = n{x^{n - 1}}$ và $\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)$
nếu $u= u\left(x\right) \ne 0$ có đạo hàm trong khoảng $J$.
5. Đạo hàm của căn thức
Hàm số $y = \sqrt[n]{x}$ có thể xem là mở rộng của hàm lũy thừa $y = {x^{\dfrac{1}{n}}}$ (tập xác định của $y = \sqrt[n]{x}$ chứa tập xác định của $y = {x^{\dfrac{1}{n}}}$ và trên tập xác định của $y = {x^{\dfrac{1}{n}}}$ thì hai hàm số trùng nhau).
Khi $n$ lẻ thì hàm số $y = \sqrt[n]{x}$ có tập xác định $R$. Trên khoảng $\left(0; +∞\right) $ ta có $y = \sqrt[n]{x} = {x^{\dfrac{1}{n}}}$ và $\left( {{x^{\dfrac{1}{n}}}} \right)' = \dfrac{1}{n}{x^{\dfrac{1}{n} - 1}}$, do đó $\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$.
Công thức này còn đúng cả với $x < 0$ và hàm số $y = \sqrt[n]{x}$ không có đạo hàm tại $x= 0$.
Khi $n$ chẵn hàm $y = \sqrt[n]{x}$ có tập xác định là $[0;+∞)$, không có đạo hàm tại $x= 0$ và có đạo hàm tại mọi $x > 0$ tính theo công thức:
$ \left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$
Tóm lại, ta có $ \left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}$ đúng với mọi $x$ làm cho hai vế có nghĩa.
Sử dụng quy tắc đạo hàm hàm hợp ta suy ra: Nếu $u=u\left(x\right)$ là hàm có đạo hàm trên khoảng $J$ và thỏa mãn điều kiện $u\left(x\right) > 0, ∀x ∈ J$ khi $n$ chẵn, $u\left( x \right) \ne 0,\forall x \in J$ khi $n$ lẻ thì
$\forall x \in J,\left( {\sqrt[n]{{u\left( x \right)}}} \right)' = \dfrac{{u'\left( x \right)}}{{n\sqrt[n]{{{u^{n - 1}}\left( x \right)}}}}$
6. Đồ thị hàm số $y = {x^\alpha }$ trên khoảng $\left(0; +∞\right)$

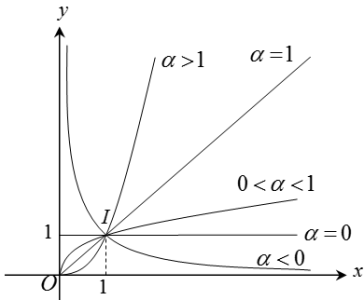
Chú ý: Khi khảo sát hàm số $y = {x^\alpha }$ với $\alpha $ cụ thể, cần xét hàm số trên toàn tập xác định của nó (chứ không phải chỉ xét trên khoảng $\left(0; +∞\right)$ như trên).