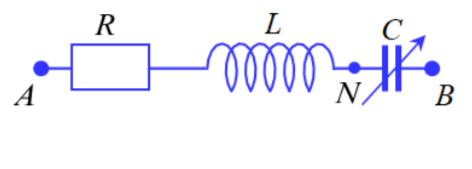
Câu hỏi: Đặt điện áp $u={{U}_{0}}\cos (100\pi t)\text{ V}$ vào hai đầu mạch điện nối tiếp như hình bên. Đoạn mạch gồm điện trở R, cuộn dây thuần cảm có độ tự cảm L, tụ điện có điện dung C thay đổi được. Khi $\text{C}={{\text{C}}_{1}}$ và $\text{C}={{\text{C}}_{2}}=0,5{{\text{C}}_{1}}$ thì điện áp tức thời ${{\text{u}}_{\text{AN}}}$ có cùng giá trị hiệu dụng nhưng lệch pha nhau 600. Cho biết $R=50\sqrt{3}\Omega ,$ điện dung C1 có giá trị là
A. $\dfrac{{{10}^{-4}}}{\pi }F$
B. $\dfrac{{{10}^{-4}}}{3\pi }F$
C. $\dfrac{{{2.10}^{-4}}}{\pi }F$
D. $\dfrac{{{10}^{-4}}}{2\pi }F$

A. $\dfrac{{{10}^{-4}}}{\pi }F$
B. $\dfrac{{{10}^{-4}}}{3\pi }F$
C. $\dfrac{{{2.10}^{-4}}}{\pi }F$
D. $\dfrac{{{10}^{-4}}}{2\pi }F$
Phương pháp:
Dung kháng của tụ điện: ${{Z}_{C}}=\dfrac{1}{\omega C}$
Điện áp hiệu dụng giữa hai đầu đoạn mạch AN: ${{u}_{AN}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$ Độ lệch pha giữa điện áp và cường độ dòng điện: $\tan \varphi =\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}$
Công thức lượng giác: $\tan (a-b)=\dfrac{\tan a-\tan b}{1+\tan a\tan b}$
Cách giải:
Ta có: ${{Z}_{C2}}=0,5{{Z}_{C1}}=\dfrac{1}{2}{{Z}_{C1}}\Rightarrow {{Z}_{C2}}=2{{Z}_{C1}}$
Điện áp hiệu dụng giữa hai đầu đoạn mạch AN là: ${{u}_{AN}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$
Khi C = C1 và C = C2, điện áp hiệu dụng giữa hai đầu đoạn mạch AN có cùng giá trị, ta có:
$\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}}}$ $\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}={{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}$
$\Rightarrow \left[ \begin{array}{*{35}{l}}
{{Z}_{L}}-{{Z}_{C1}}={{Z}_{L}}-{{Z}_{C2}}\text{ (loai)} \\
{{Z}_{L}}-{{Z}_{C1}}=-\left( {{Z}_{L}}-{{Z}_{C2}} \right) \\
\end{array} \right. $ $ \Rightarrow {{Z}_{L}}=\dfrac{{{Z}_{C1}}+{{Z}_{C2}}}{2}=\dfrac{3}{2}{{Z}_{C1}}$
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN và cường độ dòng điện là:
$\tan {{\varphi }_{AN}}=\dfrac{{{Z}_{L}}}{R}=~const~\Rightarrow {{\varphi }_{AN/i}}=~const~$
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN trong các trường hợp là:
$\Delta \varphi ={{\varphi }_{1{{u}_{AN}}}}-{{\varphi }_{2{{u}_{AN}}}}={{\varphi }_{i1}}-{{\varphi }_{i2}}=\dfrac{\pi }{3}(rad)$
Ta có: $\tan \dfrac{\pi }{3}=\tan \left( {{\varphi }_{i1}}-{{\varphi }_{i2}} \right)=\dfrac{\tan {{\varphi }_{i1}}-\tan {{\varphi }_{i2}}}{1+\tan {{\varphi }_{i1}}\tan {{\varphi }_{i2}}}$
$\Rightarrow \dfrac{\dfrac{{{Z}_{L}}-{{Z}_{C1}}}{R}-\dfrac{{{Z}_{L}}-{{Z}_{C2}}}{R}}{1+\dfrac{{{Z}_{L}}-{{Z}_{C1}}}{R}\cdot \dfrac{{{Z}_{L}}-{{Z}_{C2}}}{R}}=\dfrac{2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)}{{{R}^{2}}-{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}=\sqrt{3}$
$\Rightarrow 2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)=\sqrt{3}{{R}^{2}}-\sqrt{3}{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}\Rightarrow {{Z}_{L}}-{{Z}_{C1}}=\dfrac{R}{\sqrt{3}}=50(\Omega )$
$\Rightarrow \dfrac{3}{2}{{Z}_{C1}}-{{Z}_{C1}}=50\Rightarrow {{Z}_{C1}}=100(\Omega )$ Dung kháng của tụ điện là:
${{Z}_{C1}}=\dfrac{1}{\omega {{C}_{1}}}\Rightarrow {{C}_{1}}=\dfrac{1}{\omega {{Z}_{C1}}}=\dfrac{1}{100.100\pi }=\dfrac{{{10}^{-4}}}{\pi }(F)$
Dung kháng của tụ điện: ${{Z}_{C}}=\dfrac{1}{\omega C}$
Điện áp hiệu dụng giữa hai đầu đoạn mạch AN: ${{u}_{AN}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$ Độ lệch pha giữa điện áp và cường độ dòng điện: $\tan \varphi =\dfrac{{{Z}_{L}}-{{Z}_{C}}}{R}$
Công thức lượng giác: $\tan (a-b)=\dfrac{\tan a-\tan b}{1+\tan a\tan b}$
Cách giải:
Ta có: ${{Z}_{C2}}=0,5{{Z}_{C1}}=\dfrac{1}{2}{{Z}_{C1}}\Rightarrow {{Z}_{C2}}=2{{Z}_{C1}}$
Điện áp hiệu dụng giữa hai đầu đoạn mạch AN là: ${{u}_{AN}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$
Khi C = C1 và C = C2, điện áp hiệu dụng giữa hai đầu đoạn mạch AN có cùng giá trị, ta có:
$\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}}=\dfrac{U\sqrt{{{R}^{2}}+Z_{L}^{2}}}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}}}$ $\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}={{\left( {{Z}_{L}}-{{Z}_{C2}} \right)}^{2}}$
$\Rightarrow \left[ \begin{array}{*{35}{l}}
{{Z}_{L}}-{{Z}_{C1}}={{Z}_{L}}-{{Z}_{C2}}\text{ (loai)} \\
{{Z}_{L}}-{{Z}_{C1}}=-\left( {{Z}_{L}}-{{Z}_{C2}} \right) \\
\end{array} \right. $ $ \Rightarrow {{Z}_{L}}=\dfrac{{{Z}_{C1}}+{{Z}_{C2}}}{2}=\dfrac{3}{2}{{Z}_{C1}}$
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN và cường độ dòng điện là:
$\tan {{\varphi }_{AN}}=\dfrac{{{Z}_{L}}}{R}=~const~\Rightarrow {{\varphi }_{AN/i}}=~const~$
Độ lệch pha giữa điện áp hai đầu đoạn mạch AN trong các trường hợp là:
$\Delta \varphi ={{\varphi }_{1{{u}_{AN}}}}-{{\varphi }_{2{{u}_{AN}}}}={{\varphi }_{i1}}-{{\varphi }_{i2}}=\dfrac{\pi }{3}(rad)$
Ta có: $\tan \dfrac{\pi }{3}=\tan \left( {{\varphi }_{i1}}-{{\varphi }_{i2}} \right)=\dfrac{\tan {{\varphi }_{i1}}-\tan {{\varphi }_{i2}}}{1+\tan {{\varphi }_{i1}}\tan {{\varphi }_{i2}}}$
$\Rightarrow \dfrac{\dfrac{{{Z}_{L}}-{{Z}_{C1}}}{R}-\dfrac{{{Z}_{L}}-{{Z}_{C2}}}{R}}{1+\dfrac{{{Z}_{L}}-{{Z}_{C1}}}{R}\cdot \dfrac{{{Z}_{L}}-{{Z}_{C2}}}{R}}=\dfrac{2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)}{{{R}^{2}}-{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}}=\sqrt{3}$
$\Rightarrow 2R\left( {{Z}_{L}}-{{Z}_{C1}} \right)=\sqrt{3}{{R}^{2}}-\sqrt{3}{{\left( {{Z}_{L}}-{{Z}_{C1}} \right)}^{2}}\Rightarrow {{Z}_{L}}-{{Z}_{C1}}=\dfrac{R}{\sqrt{3}}=50(\Omega )$
$\Rightarrow \dfrac{3}{2}{{Z}_{C1}}-{{Z}_{C1}}=50\Rightarrow {{Z}_{C1}}=100(\Omega )$ Dung kháng của tụ điện là:
${{Z}_{C1}}=\dfrac{1}{\omega {{C}_{1}}}\Rightarrow {{C}_{1}}=\dfrac{1}{\omega {{Z}_{C1}}}=\dfrac{1}{100.100\pi }=\dfrac{{{10}^{-4}}}{\pi }(F)$
Đáp án A.