Câu hỏi: Đặt điện áp $u=100\sqrt{2}\cos \left( 100\pi t \right)\left( \text{V} \right)$ vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Thay đổi C để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại; khi đó điện áp hiệu dụng giữa hai đầu cuộn cảm là ${{U}_{L}}=97,5V\left( \text{V} \right)$. So với điện áp hai đầu đoạn mạch thì điện áp hai đầu điện trở thuần
A. sớm pha hơn một góc $0,22\pi $
B. sớm pha hơn $0,25\pi $
C. trễ pha hơn một góc $0,22\pi $
D. trễ pha hơn một góc $0,25\pi $
A. sớm pha hơn một góc $0,22\pi $
B. sớm pha hơn $0,25\pi $
C. trễ pha hơn một góc $0,22\pi $
D. trễ pha hơn một góc $0,25\pi $
Khi C biến thiên để ${{U}_{C}}$ cực đại thì điện áp giữa hai đầu đoạn mạch u vuông pha với điện áp giữa hai đầu đoạn mạch RL.
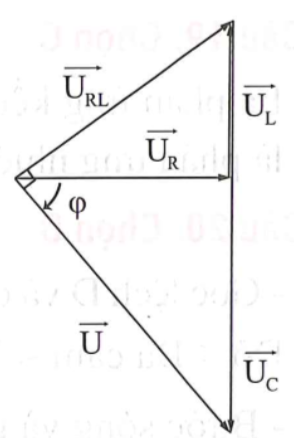
Từ hình vẽ, áp dụng hệ thức lượng trong tam giác vuông ta có:
${{U}^{2}}={{U}_{C}}.\left( {{U}_{C}}-{{U}_{L}} \right)\Leftrightarrow {{100}^{2}}={{U}_{C}}\left( {{U}_{C}}-97,5 \right)\Rightarrow {{U}_{C}}=160V$
$\sin \varphi =\dfrac{{{U}_{C}}-{{U}_{L}}}{U}=\dfrac{160-97,5}{100}=0,625\Rightarrow \varphi =0,22\pi $
Điện áp hai đầu điện trở sớm pha hơn điện áp hai đầu đoạn mạch một góc $0,22\pi $
[/TD][TD]
[/TD][/TR][/TABLE]Bài toán cực trị của dòng điện xoay chiều khi C thay đổi:
- Cộng hưởng khi: ${{Z}_{L}}={{Z}_{C}}$ thì các giá trị ${{I}_{\max }},{{P}_{\max }},\cos {{\varphi }_{\max }},{{Z}_{\min }},{{U}_{R\max }},{{U}_{RL\max }},{{U}_{L\max }}$
Khi đó: ${{I}_{\max }}=\dfrac{U}{R},{{P}_{\max }}=\dfrac{{{U}^{2}}}{R},\cos {{\varphi }_{\max }}=1,{{Z}_{\min }}=R$
- Bài toán có hai giá trị ${{Z}_{C1}},{{Z}_{C2}}$ cho cùng $I,P,{{U}_{R}},{{U}_{RL}},{{U}_{L}},\cos \varphi $
Khi đó: ${{Z}_{C1}}+{{Z}_{C2}}=2{{Z}_{L}}$
- Khi ${{Z}_{C}}={{Z}_{C0}}$ để ${{U}_{C\max }}$ thì ${{u}_{RL}}\bot u$, khi đó: ${{Z}_{C0}}=\dfrac{{{R}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}$, ${{U}_{C\max }}=\dfrac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}$
- Thay đổi C có ${{Z}_{C1}},{{Z}_{C2}}$ cùng ${{U}_{C}}$, khi đó:
$\left\{ \begin{aligned}
& \dfrac{1}{{{Z}_{C1}}}+\dfrac{1}{{{Z}_{C2}}}=\dfrac{2}{{{Z}_{C0}}} \\
& {{U}_{C}}={{U}_{C\max }}\cos \left( {{\varphi }_{0}}-{{\varphi }_{1}} \right)={{U}_{C\max }}\cos \left( {{\varphi }_{0}}-{{\varphi }_{2}} \right) \\
\end{aligned} \right.$
- Thay đổi C để ${{U}_{RC}}\max $, khi đó: ${{Z}_{C}}=\dfrac{{{Z}_{L}}+\sqrt{4{{R}^{2}}+Z_{C}^{2}}}{2}$, ${{U}_{RC\max }}=\dfrac{2UR}{\sqrt{4{{R}^{2}}+Z_{L}^{2}-{{Z}_{L}}}}$.
Từ hình vẽ, áp dụng hệ thức lượng trong tam giác vuông ta có:
${{U}^{2}}={{U}_{C}}.\left( {{U}_{C}}-{{U}_{L}} \right)\Leftrightarrow {{100}^{2}}={{U}_{C}}\left( {{U}_{C}}-97,5 \right)\Rightarrow {{U}_{C}}=160V$
$\sin \varphi =\dfrac{{{U}_{C}}-{{U}_{L}}}{U}=\dfrac{160-97,5}{100}=0,625\Rightarrow \varphi =0,22\pi $
Điện áp hai đầu điện trở sớm pha hơn điện áp hai đầu đoạn mạch một góc $0,22\pi $
[/TD][TD]
[/TD][/TR][/TABLE]Bài toán cực trị của dòng điện xoay chiều khi C thay đổi:
- Cộng hưởng khi: ${{Z}_{L}}={{Z}_{C}}$ thì các giá trị ${{I}_{\max }},{{P}_{\max }},\cos {{\varphi }_{\max }},{{Z}_{\min }},{{U}_{R\max }},{{U}_{RL\max }},{{U}_{L\max }}$
Khi đó: ${{I}_{\max }}=\dfrac{U}{R},{{P}_{\max }}=\dfrac{{{U}^{2}}}{R},\cos {{\varphi }_{\max }}=1,{{Z}_{\min }}=R$
- Bài toán có hai giá trị ${{Z}_{C1}},{{Z}_{C2}}$ cho cùng $I,P,{{U}_{R}},{{U}_{RL}},{{U}_{L}},\cos \varphi $
Khi đó: ${{Z}_{C1}}+{{Z}_{C2}}=2{{Z}_{L}}$
- Khi ${{Z}_{C}}={{Z}_{C0}}$ để ${{U}_{C\max }}$ thì ${{u}_{RL}}\bot u$, khi đó: ${{Z}_{C0}}=\dfrac{{{R}^{2}}+Z_{L}^{2}}{{{Z}_{L}}}$, ${{U}_{C\max }}=\dfrac{U\sqrt{{{R}^{2}}+Z_{C}^{2}}}{R}$
- Thay đổi C có ${{Z}_{C1}},{{Z}_{C2}}$ cùng ${{U}_{C}}$, khi đó:
$\left\{ \begin{aligned}
& \dfrac{1}{{{Z}_{C1}}}+\dfrac{1}{{{Z}_{C2}}}=\dfrac{2}{{{Z}_{C0}}} \\
& {{U}_{C}}={{U}_{C\max }}\cos \left( {{\varphi }_{0}}-{{\varphi }_{1}} \right)={{U}_{C\max }}\cos \left( {{\varphi }_{0}}-{{\varphi }_{2}} \right) \\
\end{aligned} \right.$
- Thay đổi C để ${{U}_{RC}}\max $, khi đó: ${{Z}_{C}}=\dfrac{{{Z}_{L}}+\sqrt{4{{R}^{2}}+Z_{C}^{2}}}{2}$, ${{U}_{RC\max }}=\dfrac{2UR}{\sqrt{4{{R}^{2}}+Z_{L}^{2}-{{Z}_{L}}}}$.
Đáp án A.