liked
Well-Known Member
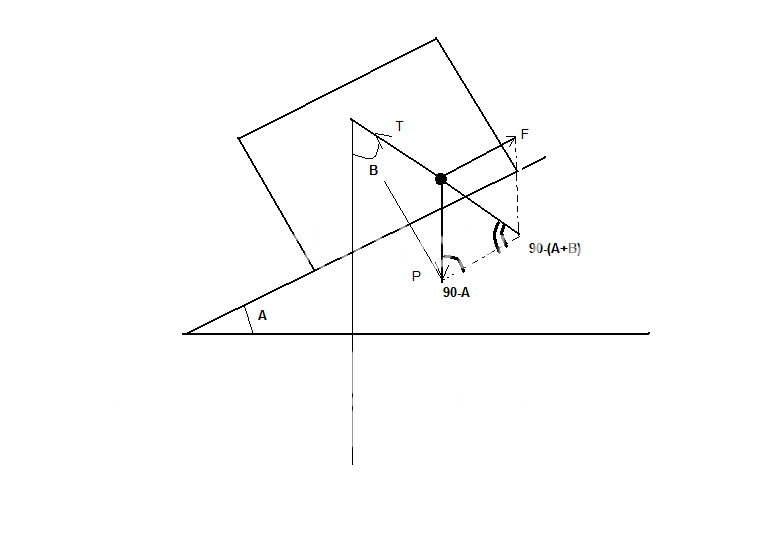
Bài toán 1 con lắc đơn chiều dài l được treo vào trần của 1 toa xe đang xuống dốc mà mặt dốc nghiêng một góc $\alpha$ so với phương ngang. Bỏ qua sức cản không khí, khi con lắc đang cân bằng trong toa xe thì dây treo nghiêng 1 góc $\beta$ so với phương thẳng đứng.Chu kì dao động nhỏ của con lắc trong toa xe là:
A.$T=2\pi\sqrt{\dfrac{l\cos(\alpha-\beta)}{g\cos\beta}}$
B.$T=2\pi\sqrt{\dfrac{l\cos(\alpha+\beta)}{g\cos\alpha}}$
C.$T=2\pi\sqrt{\dfrac{l\cos(\alpha-\beta)}{g\cos\alpha}}$
D.$T=2\pi\sqrt{\dfrac{l\cos(\alpha+\beta)}{g\cos\beta}}$
A.$T=2\pi\sqrt{\dfrac{l\cos(\alpha-\beta)}{g\cos\beta}}$
B.$T=2\pi\sqrt{\dfrac{l\cos(\alpha+\beta)}{g\cos\alpha}}$
C.$T=2\pi\sqrt{\dfrac{l\cos(\alpha-\beta)}{g\cos\alpha}}$
D.$T=2\pi\sqrt{\dfrac{l\cos(\alpha+\beta)}{g\cos\beta}}$
Lần chỉnh sửa cuối bởi 1 quản trị viên: