Câu hỏi: Cho hình chóp tứ giác đều \(S. ABCD\), đáy là hình vuông cạnh \(a\), cạnh bên tạo với đáy một góc \(60^0\). Gọi \(M\) là trung điểm \(SC\). Mặt phẳng đi qua \(AM\) và song song với \(BD\), cắt \(SB\) tại \(E\) và cắt \(SD\) tại \(F\). Tính thể tích khối chóp \(S. AEMF\).
Phương pháp giải
Hình chóp đều có chân đường cao trùng với tâm của đáy.
Xác định thiết diện của hình chóp cắt bởi mặt phẳng đi qua AM và song song với BD là tức giác AEMF.
Chứng minh AEMF có hai đường chéo vuông góc \(\Rightarrow {S_{AEMF}} = \dfrac{1}{2}AM. EF\)
Chứng minh \(SM \bot \left( {AEMF} \right)\) \(\Rightarrow {V_{S. AEMF}} = \dfrac{1}{3}SM.{S_{AEMF}}\)
Lời giải chi tiết
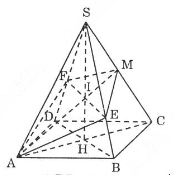
Gọi \(\displaystyle H = AC \cap BD\).
Hình chóp \(\displaystyle S. ABCD\) là hình chóp đều nên chân \(\displaystyle H\) của đường cao \(\displaystyle SH\) chính là tâm của đáy.
Mặt phẳng đi qua \(\displaystyle AM\) và song song với \(\displaystyle BD\) cắt mặt phẳng \(\displaystyle (SDB)\) theo một giao tuyến song song với \(\displaystyle BD\)\. Ta dựng giao tuyến \(\displaystyle EF\) như sau: Gọi \(\displaystyle I\) là giao điểm của \(\displaystyle AM\) và \(\displaystyle SH\). Qua \(\displaystyle I\) ta dựng một đường thẳng song song với \(\displaystyle BD\), đường này cắt \(\displaystyle SB\) ở \(\displaystyle E\) và cắt \(\displaystyle SD\) ở \(\displaystyle F\).
Ta có: \(\displaystyle HA\) là hình chiếu vuông góc của \(\displaystyle SA\) trên \(\displaystyle (ABCD)\) \(\displaystyle \Rightarrow \widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {\left({SA; AH} \right)} = \widehat {SAH} = {60^0}\)
Tam giác cân \(\displaystyle SAC\) có \(\displaystyle SA = SC\) và góc \(\displaystyle SAC = 60^0\) nên nó là tam giác đều: \(\displaystyle I\) là giao điểm của các trung tuyến \(\displaystyle AM\) và \(\displaystyle AH\) nên I là trọng tâm của tam giác đều SAC \(\displaystyle \Rightarrow {{SI} \over {SH}} = {2 \over 3}\)
Do \(\displaystyle EF // DB \) \(\displaystyle \Rightarrow {{{\rm{EF}}} \over {DB}} = {{SF} \over {SD}} = {{SE} \over {SB}} = {{SI} \over {SH}} = {2 \over 3}\)
Vì \(\displaystyle DB = a\sqrt2\) \(\displaystyle \Rightarrow {\rm{EF}} = {{2a\sqrt 2 } \over 3}\)
Tam giác \(\displaystyle SAC\) là tam giác đều nên \(\displaystyle AM = {{AC\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\)
Ta lại có \(\displaystyle \left\{ \begin{array}{l}BD \bot AC\\BD \bot SH\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \) \(\Rightarrow BD \bot AM \Rightarrow AM \bot EF\)
Tứ giác \(\displaystyle AEMF\) có hai đường chéo vuông góc với nhau nên có diện tích: \(\displaystyle {S_{AEMF}} = {1 \over 2}{\rm{EF}}. AM = {1 \over 2}.{{2a\sqrt 2 } \over 3}.{{a\sqrt 6 } \over 2} = {{{a^2}\sqrt 3 } \over 3}\)
Mặt khác, tam giác \(\displaystyle ASC\) là tam giác đều, \(\displaystyle M\) là trung điểm của \(\displaystyle SC\) nên \(\displaystyle AM \bot SC\). Ta cũng có \(\displaystyle DB \bot (SAM)\) \(\displaystyle \Rightarrow DB \bot SC\) vì \(\displaystyle DB // EF\) nên \(\displaystyle EF \bot SC\). Từ kết quả trên, suy ra \(\displaystyle SM \bot(AEMF)\).
Dễ thấy \(\displaystyle SM = {{a\sqrt 2 } \over 2}\) (do tam giác \(\displaystyle SAC\) đều). Do đó: \(\displaystyle {V_{S. AEMF}} = {1 \over 3}.{{{a^2}\sqrt 3 } \over 3}.{{a\sqrt 2 } \over 2} = {{{a^3}\sqrt 6 } \over {18}}\).
Hình chóp đều có chân đường cao trùng với tâm của đáy.
Xác định thiết diện của hình chóp cắt bởi mặt phẳng đi qua AM và song song với BD là tức giác AEMF.
Chứng minh AEMF có hai đường chéo vuông góc \(\Rightarrow {S_{AEMF}} = \dfrac{1}{2}AM. EF\)
Chứng minh \(SM \bot \left( {AEMF} \right)\) \(\Rightarrow {V_{S. AEMF}} = \dfrac{1}{3}SM.{S_{AEMF}}\)
Lời giải chi tiết
Gọi \(\displaystyle H = AC \cap BD\).
Hình chóp \(\displaystyle S. ABCD\) là hình chóp đều nên chân \(\displaystyle H\) của đường cao \(\displaystyle SH\) chính là tâm của đáy.
Mặt phẳng đi qua \(\displaystyle AM\) và song song với \(\displaystyle BD\) cắt mặt phẳng \(\displaystyle (SDB)\) theo một giao tuyến song song với \(\displaystyle BD\)\. Ta dựng giao tuyến \(\displaystyle EF\) như sau: Gọi \(\displaystyle I\) là giao điểm của \(\displaystyle AM\) và \(\displaystyle SH\). Qua \(\displaystyle I\) ta dựng một đường thẳng song song với \(\displaystyle BD\), đường này cắt \(\displaystyle SB\) ở \(\displaystyle E\) và cắt \(\displaystyle SD\) ở \(\displaystyle F\).
Ta có: \(\displaystyle HA\) là hình chiếu vuông góc của \(\displaystyle SA\) trên \(\displaystyle (ABCD)\) \(\displaystyle \Rightarrow \widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {\left({SA; AH} \right)} = \widehat {SAH} = {60^0}\)
Tam giác cân \(\displaystyle SAC\) có \(\displaystyle SA = SC\) và góc \(\displaystyle SAC = 60^0\) nên nó là tam giác đều: \(\displaystyle I\) là giao điểm của các trung tuyến \(\displaystyle AM\) và \(\displaystyle AH\) nên I là trọng tâm của tam giác đều SAC \(\displaystyle \Rightarrow {{SI} \over {SH}} = {2 \over 3}\)
Do \(\displaystyle EF // DB \) \(\displaystyle \Rightarrow {{{\rm{EF}}} \over {DB}} = {{SF} \over {SD}} = {{SE} \over {SB}} = {{SI} \over {SH}} = {2 \over 3}\)
Vì \(\displaystyle DB = a\sqrt2\) \(\displaystyle \Rightarrow {\rm{EF}} = {{2a\sqrt 2 } \over 3}\)
Tam giác \(\displaystyle SAC\) là tam giác đều nên \(\displaystyle AM = {{AC\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\)
Ta lại có \(\displaystyle \left\{ \begin{array}{l}BD \bot AC\\BD \bot SH\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \) \(\Rightarrow BD \bot AM \Rightarrow AM \bot EF\)
Tứ giác \(\displaystyle AEMF\) có hai đường chéo vuông góc với nhau nên có diện tích: \(\displaystyle {S_{AEMF}} = {1 \over 2}{\rm{EF}}. AM = {1 \over 2}.{{2a\sqrt 2 } \over 3}.{{a\sqrt 6 } \over 2} = {{{a^2}\sqrt 3 } \over 3}\)
Mặt khác, tam giác \(\displaystyle ASC\) là tam giác đều, \(\displaystyle M\) là trung điểm của \(\displaystyle SC\) nên \(\displaystyle AM \bot SC\). Ta cũng có \(\displaystyle DB \bot (SAM)\) \(\displaystyle \Rightarrow DB \bot SC\) vì \(\displaystyle DB // EF\) nên \(\displaystyle EF \bot SC\). Từ kết quả trên, suy ra \(\displaystyle SM \bot(AEMF)\).
Dễ thấy \(\displaystyle SM = {{a\sqrt 2 } \over 2}\) (do tam giác \(\displaystyle SAC\) đều). Do đó: \(\displaystyle {V_{S. AEMF}} = {1 \over 3}.{{{a^2}\sqrt 3 } \over 3}.{{a\sqrt 2 } \over 2} = {{{a^3}\sqrt 6 } \over {18}}\).