Câu hỏi: Cho hình chóp tam giác \(O. ABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc với nhau và \(OA = a, OB = b, OC = c\). Hãy tính đường cao \(OH\) của hình chóp.
Phương pháp giải
+) Gọi \(H\) là trọng tâm của \(\Delta{ABC}\), chứng minh \(OH \bot (ABC)\).
+) Sử dụng các hệ thức lượng trong tam giác vuông tính \(OH\).
Lời giải chi tiết
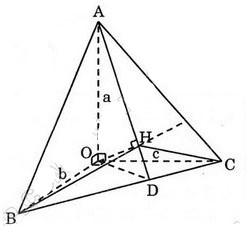
Kẻ \(\displaystyle AD\bot BC, OH \bot AD\) ta chứng minh \(\displaystyle OH\) chính là đường cao của hình chóp.
\(\displaystyle \begin{array}{l}
\left\{ \begin{array}{l}
BC \bot OA\\
BC \bot AH
\end{array} \right. \Rightarrow BC \bot \left({OAH} \right) \\\Rightarrow BC \bot OH \left(1 \right)\\
\left\{ \begin{array}{l}
AC \bot BH\\
AC \bot OB
\end{array} \right. \Rightarrow AC \bot \left({OBH} \right) \\\Rightarrow AC \bot OH \left(2 \right)\\
\left(1 \right);\left(2 \right) \Rightarrow OH \bot \left({ABC} \right)
\end{array}\)
Vậy \(\displaystyle OH\) chính là đường cao của hình chóp.
\(\displaystyle BC \bot \left( {OAH} \right) \Rightarrow BC \bot \left({OAD} \right) \) \(\Rightarrow BC \bot OD\).
Tam giác OBC vuông tại O nên \(BC = \sqrt {O{B^2} + O{C^2}} = \sqrt {{b^2} + {c^2}} \)
Áp dụng hệ thức lượng trong tam giác vuông OBC ta có:
\(\displaystyle OD. BC = OB. OC\) nên \(\displaystyle OD = \frac{{OB. OC}}{{BC}}={{bc} \over {\sqrt {{b^2} + {c^2}} }}\).
Áp dụng định lí Pitago trong tam giác vuông OAD ta có:
\(\displaystyle AD = \sqrt {A{O^2} + O{D^2}} \) \(= \sqrt {{a^2} + {{{b^2}{c^2}} \over {{b^2} + {c^2}}}}\)
\(\displaystyle = \sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}\) .
Áp dụng hệ thức lượng trong tam giác vuông OAD ta có: \(\displaystyle OH. AD = OA. OD\) nên
\(\displaystyle OH = \frac{{OA. OD}}{{AD}}\) \(= {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}} \) \(\displaystyle = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\).
Cách khác:
Tam giác OBC vuông tại O có OD là đường cao nên \(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Tam giác AOD vuông tại O có chiều cao OH nên
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}}\) \( = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\) \(= \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{b^2}{c^2} + {c^2}{a^2} + {a^2}{b^2}}}{{{a^2}{b^2}{c^2}}}\)
\(\Rightarrow O{H^2} = \frac{{{a^2}{b^2}{c^2}}}{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}\)
\(\Rightarrow OH = \frac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Chú ý: Ta thấy khi OABC là tứ diện vuông (OA, OB, OC đôi một vuông góc) thì: \(\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Từ nay về sau các em sử dụng kết quả này để các bài toán nhanh chóng hơn.
+) Gọi \(H\) là trọng tâm của \(\Delta{ABC}\), chứng minh \(OH \bot (ABC)\).
+) Sử dụng các hệ thức lượng trong tam giác vuông tính \(OH\).
Lời giải chi tiết
Kẻ \(\displaystyle AD\bot BC, OH \bot AD\) ta chứng minh \(\displaystyle OH\) chính là đường cao của hình chóp.
\(\displaystyle \begin{array}{l}
\left\{ \begin{array}{l}
BC \bot OA\\
BC \bot AH
\end{array} \right. \Rightarrow BC \bot \left({OAH} \right) \\\Rightarrow BC \bot OH \left(1 \right)\\
\left\{ \begin{array}{l}
AC \bot BH\\
AC \bot OB
\end{array} \right. \Rightarrow AC \bot \left({OBH} \right) \\\Rightarrow AC \bot OH \left(2 \right)\\
\left(1 \right);\left(2 \right) \Rightarrow OH \bot \left({ABC} \right)
\end{array}\)
Vậy \(\displaystyle OH\) chính là đường cao của hình chóp.
\(\displaystyle BC \bot \left( {OAH} \right) \Rightarrow BC \bot \left({OAD} \right) \) \(\Rightarrow BC \bot OD\).
Tam giác OBC vuông tại O nên \(BC = \sqrt {O{B^2} + O{C^2}} = \sqrt {{b^2} + {c^2}} \)
Áp dụng hệ thức lượng trong tam giác vuông OBC ta có:
\(\displaystyle OD. BC = OB. OC\) nên \(\displaystyle OD = \frac{{OB. OC}}{{BC}}={{bc} \over {\sqrt {{b^2} + {c^2}} }}\).
Áp dụng định lí Pitago trong tam giác vuông OAD ta có:
\(\displaystyle AD = \sqrt {A{O^2} + O{D^2}} \) \(= \sqrt {{a^2} + {{{b^2}{c^2}} \over {{b^2} + {c^2}}}}\)
\(\displaystyle = \sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}\) .
Áp dụng hệ thức lượng trong tam giác vuông OAD ta có: \(\displaystyle OH. AD = OA. OD\) nên
\(\displaystyle OH = \frac{{OA. OD}}{{AD}}\) \(= {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}} \) \(\displaystyle = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\).
Cách khác:
Tam giác OBC vuông tại O có OD là đường cao nên \(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Tam giác AOD vuông tại O có chiều cao OH nên
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}}\) \( = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\) \(= \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{b^2}{c^2} + {c^2}{a^2} + {a^2}{b^2}}}{{{a^2}{b^2}{c^2}}}\)
\(\Rightarrow O{H^2} = \frac{{{a^2}{b^2}{c^2}}}{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}\)
\(\Rightarrow OH = \frac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Chú ý: Ta thấy khi OABC là tứ diện vuông (OA, OB, OC đôi một vuông góc) thì: \(\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Từ nay về sau các em sử dụng kết quả này để các bài toán nhanh chóng hơn.