Câu hỏi:
Phương pháp giải:
Khảo sát và vẽ đồ thi qua các bước đã được học.
Lời giải chi tiết:
Xét hàm số: $\displaystyle y = {{x + 3} \over {x + 1}}$
Tập xác định : $\displaystyle D=\mathbb R\backslash {\rm{\{ }} - 1\} $
* Sự biến thiên:
$\displaystyle y' = {{ - 2} \over {{{\left(x + 1\right)}^2}}} < 0,\forall x \in D$
- Hàm số nghịch biến trên khoảng: $\displaystyle \left(-\infty;-1\right)$ và $\displaystyle \left(-1;+\infty\right)$
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
$\displaystyle \eqalign{& \mathop {\lim }\limits_{x \Rightarrow - {1^ - }} y = - \infty \cr & \mathop {\lim }\limits_{x \Rightarrow - {1^ + }} y = + \infty \cr & \mathop {\lim }\limits_{x \Rightarrow \pm \infty } y = 1 \cr} $
Tiệm cận đứng: $\displaystyle x = -1.$
Tiệm cận ngang: $\displaystyle y = 1.$
Bảng biến thiên:
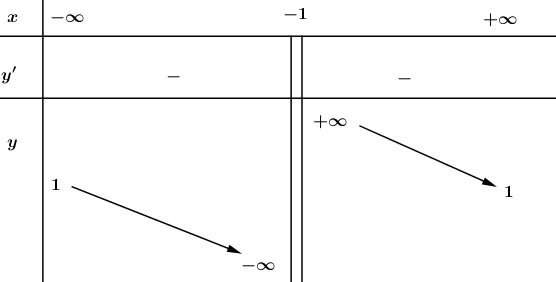
* Đồ thị:
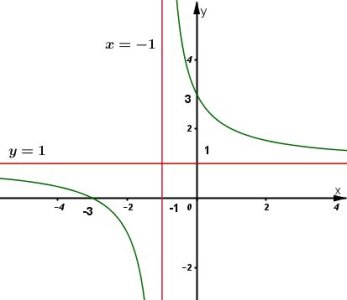
Đồ thị hàm số giao $\displaystyle Ox$ tại $\displaystyle \left(-3;0\right)$, giao $\displaystyle Oy$ tại $\displaystyle \left(0;3\right)$
Đồ thị hàm số nhận điểm $\displaystyle I\left(-1;1\right)$ làm tâm đối xứng.
Phương pháp giải:
Chứng minh phương trình hoành độ giao điểm của hai đồ thị hàm số có hai nghiệm phân biệt khác $\displaystyle -1$ với mọi $\displaystyle m.$
Lời giải chi tiết:
Xét phương trình có nghiệm là hoành độ giao điểm của $\displaystyle \left(C\right)$ và đường thẳng (d): $\displaystyle y = 2x + m$ (1)
$\displaystyle \eqalign{
& {{x + 3} \over {x + 1}} = 2x + m \Leftrightarrow x + 3 = \left(2x + m\right)\left(x + 1\right) \cr
& \Leftrightarrow 2{x^2} + \left(m + 1\right)x + m - 3 = 0,x \ne - 1 \cr} $
$\displaystyle Δ = \left(m+1\right)^2– 4.2\left(m-3\right) \\ = m^2+2m+1-8m+24 \\= m^2– 6m + 25\\ = \left(m-3\right)^2+ 16> 0 $
$\displaystyle \Rightarrow $ (1) luôn có hai nghiệm phân biệt.
Lại có: $\displaystyle f\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} - \left( {m + 1} \right) + m - 3 = - 2 \ne 0$ hay phương trình (1) có nghiệm khác $\displaystyle -1$.
Vậy phương trình (1) luôn có 2 nghiệm phân biệt khác $\displaystyle -1$ với mọi $\displaystyle m.$
Vậy (d) luôn cắt (C) tại hai điểm phân biệt $\displaystyle M, N$ (hoành độ của $\displaystyle M, N$ chính là nghiệm của (1)).
Phương pháp giải:
Với hai điểm $\displaystyle M$ và $\displaystyle N$ tìm được ở câu trên, tính độ dài đoạn thẳng $\displaystyle MN$ theo công thức: $\displaystyle MN = \sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2}} = \sqrt {f\left( x \right)} .$
+) Khảo sát và tìm giá trị nhỏ nhất của hàm số $\displaystyle y=f\left(x\right)$ từ đó suy ra độ dài nhỏ nhất của $\displaystyle MN.$
Lời giải chi tiết:
Gọi $\displaystyle M\left( {{x_M}; {y_M}} \right)$ và $\displaystyle N\left( {{x_N}; {y_N}} \right)$ là hai giao điểm của $\displaystyle \left(C\right)$ và đường tahnwgr $\displaystyle y=2x+m.$
Theo định lí Vi-et ta có: $\displaystyle \left\{ \matrix{{x_M} + {x_N} = - {{m + 1} \over 2} \hfill \cr {x_M}.{x_N} = {{m - 3} \over 2} \hfill \cr} \right.$
$\displaystyle \begin{array}{l}
M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + {\left[ {2{x_M} + m - \left( {2{x_N} + m} \right)} \right]^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + 4{\left( {{x_M} - {x_N}} \right)^2}\\
= 5{\left( {{x_M} - {x_N}} \right)^2}\\
= 5\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\
= 5\left[ {{{\left( { - \dfrac{{m + 1}}{2}} \right)}^2} - 4.\dfrac{{m - 3}}{2}} \right]\\
= 5\left( {\dfrac{{{m^2} + 2m + 1}}{4} - 2m + 6} \right)\\
= 5.\dfrac{{{m^2} - 6m + 25}}{4} \\ = \dfrac{5}{4}\left[ {\left( {{m^2} - 6m + 9} \right) + 16} \right]\\
= \dfrac{5}{4}\left[ {{{\left( {m - 3} \right)}^2} + 16} \right].
\end{array}$
Ta có: $\displaystyle {\left( {m - 3} \right)^2} \ge 0 \forall m \Rightarrow {\left( {m - 3} \right)^2} + 16 \ge 16$
$\displaystyle \begin{array}{l}
\Rightarrow M{N^2} \ge \dfrac{5}{4}.16 = 20.\\
\Rightarrow MN \ge 2\sqrt 5 .
\end{array}$
Dấu "=" xảy ra $\displaystyle \Leftrightarrow m - 3 = 0 \Leftrightarrow m = 3.$
Vậy độ dài $\displaystyle MN$ nhỏ nhất bằng $\displaystyle 2\sqrt5$ khi $\displaystyle m=3.$
Phương pháp giải:
Gọi $\displaystyle S\left(x_0; y_0\right)$ là 1 điểm bất kì thuộc đồ thị hàm số $\displaystyle \left(C\right).$ Khi đó phương trình tiếp tuyến của đồ thị hàm số tại $\displaystyle S$ là: $\displaystyle \Delta: y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.$
+) Tìm các giao điểm $\displaystyle P, Q$ của tiếp tuyến $\displaystyle \Delta$ với các đường tiệm cận.
+) Khi đó $\displaystyle S$ là trung điểm của $\displaystyle PQ\Leftrightarrow \left\{ \begin{array}{l}{x_0} = \dfrac{{{x_P} + {x_Q}}}{2}\\{y_0} = \dfrac{{{y_P} + {y_Q}}}{2}\end{array} \right..$
Lời giải chi tiết:
Giả sử $\displaystyle S\left(x_0;y_0\right)$ là điểm bất kì thuộc (C)
Phương trình tiếp tuyến $\displaystyle Δ$ của (C) tại $\displaystyle S$ là:
$\displaystyle \eqalign{
& y - y_0 = y'\left({x_0}\right)\left(x - {x_0}\right) \cr
& \Leftrightarrow y = {{ - 2} \over {{{\left({x_0} + 1\right)}^2}}}\left(x - {x_0}\right) + {{{x_0} + 3} \over {{x_0} + 1}} \cr} $
Tiệm cận đứng: $\displaystyle x=-1$ và tiệm cận ngang: $\displaystyle y=1.$
Giả sử $\displaystyle Δ$ cắt tiệm cận ngang tại $\displaystyle P\left(x_P; 1\right)$. Khi đó:
$\displaystyle \begin{array}{l}
\dfrac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( {{x_P} - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} + 1}} = 1\\
\Leftrightarrow - 2{x_P} + 2{x_0} + x_0^2 + 4{x_0} + 3 = x_0^2 + 2{x_0} + 1\\
\Leftrightarrow - 2{x_P} = - 4{x_0} - 2\\
\Leftrightarrow {x_P} = 2{x_0} + 1\\
\Rightarrow P\left( {2{x_0} + 1; 1} \right).
\end{array}$
$\displaystyle Δ$ cắt tiệm cận đứng tại $\displaystyle Q\left( - 1; y_Q\right).$ Khi đó:
$\displaystyle \begin{array}{l}
\dfrac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( { - 1 - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} + 1}} = {y_Q}\\
\Leftrightarrow 2 + 2{x_0} + x_0^2 + 4{x_0} + 3 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow x_0^2 + 6{x_0} + 5 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow \left( {{x_0} + 1} \right)\left( {{x_0} + 5} \right) = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow {y_Q} = \dfrac{{{x_0} + 5}}{{{x_0} + 1}}.\\
\Rightarrow Q\left( { - 1; \dfrac{{{x_0} + 5}}{{{x_0} + 1}}} \right)
\end{array}$
$\displaystyle \Rightarrow \left\{ \begin{array}{l}
{x_P} + {x_Q} = 2{x_0} + 1 - 1 = 2{x_0} = 2{x_S}\\
{y_P} + {y_Q} = 1 + \dfrac{{{x_0} + 5}}{{{x_0} + 1}} = \dfrac{{2{x_0} + 6}}{{{x_0} + 1}} = \dfrac{{2\left( {{x_0} + 3} \right)}}{{{x_0} + 1}} = 2{y_0} = 2{y_S}.
\end{array} \right.$
Vậy $\displaystyle S$ là trung điểm của $\displaystyle PQ$.
Câu a
a) Khảo sát sự biến thiên và vẽ đồ thị $\displaystyle \left(C\right)$ của hàm số $\displaystyle y = {{x + 3} \over {x + 1}}.$Phương pháp giải:
Khảo sát và vẽ đồ thi qua các bước đã được học.
Lời giải chi tiết:
Xét hàm số: $\displaystyle y = {{x + 3} \over {x + 1}}$
Tập xác định : $\displaystyle D=\mathbb R\backslash {\rm{\{ }} - 1\} $
* Sự biến thiên:
$\displaystyle y' = {{ - 2} \over {{{\left(x + 1\right)}^2}}} < 0,\forall x \in D$
- Hàm số nghịch biến trên khoảng: $\displaystyle \left(-\infty;-1\right)$ và $\displaystyle \left(-1;+\infty\right)$
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
$\displaystyle \eqalign{& \mathop {\lim }\limits_{x \Rightarrow - {1^ - }} y = - \infty \cr & \mathop {\lim }\limits_{x \Rightarrow - {1^ + }} y = + \infty \cr & \mathop {\lim }\limits_{x \Rightarrow \pm \infty } y = 1 \cr} $
Tiệm cận đứng: $\displaystyle x = -1.$
Tiệm cận ngang: $\displaystyle y = 1.$
Bảng biến thiên:

* Đồ thị:
Đồ thị hàm số giao $\displaystyle Ox$ tại $\displaystyle \left(-3;0\right)$, giao $\displaystyle Oy$ tại $\displaystyle \left(0;3\right)$
Đồ thị hàm số nhận điểm $\displaystyle I\left(-1;1\right)$ làm tâm đối xứng.

Câu b
b) Chứng minh rằng với mọi giá trị của $\displaystyle m$, đường thẳng $\displaystyle y = 2x + m$ luôn cắt $\displaystyle \left(C\right)$ tại hai điểm phân biệt $\displaystyle M$ và $\displaystyle N.$Phương pháp giải:
Chứng minh phương trình hoành độ giao điểm của hai đồ thị hàm số có hai nghiệm phân biệt khác $\displaystyle -1$ với mọi $\displaystyle m.$
Lời giải chi tiết:
Xét phương trình có nghiệm là hoành độ giao điểm của $\displaystyle \left(C\right)$ và đường thẳng (d): $\displaystyle y = 2x + m$ (1)
$\displaystyle \eqalign{
& {{x + 3} \over {x + 1}} = 2x + m \Leftrightarrow x + 3 = \left(2x + m\right)\left(x + 1\right) \cr
& \Leftrightarrow 2{x^2} + \left(m + 1\right)x + m - 3 = 0,x \ne - 1 \cr} $
$\displaystyle Δ = \left(m+1\right)^2– 4.2\left(m-3\right) \\ = m^2+2m+1-8m+24 \\= m^2– 6m + 25\\ = \left(m-3\right)^2+ 16> 0 $
$\displaystyle \Rightarrow $ (1) luôn có hai nghiệm phân biệt.
Lại có: $\displaystyle f\left( { - 1} \right) = 2.{\left( { - 1} \right)^2} - \left( {m + 1} \right) + m - 3 = - 2 \ne 0$ hay phương trình (1) có nghiệm khác $\displaystyle -1$.
Vậy phương trình (1) luôn có 2 nghiệm phân biệt khác $\displaystyle -1$ với mọi $\displaystyle m.$
Vậy (d) luôn cắt (C) tại hai điểm phân biệt $\displaystyle M, N$ (hoành độ của $\displaystyle M, N$ chính là nghiệm của (1)).
Câu c
c) Xác định m sao cho độ dài $\displaystyle MN$ là nhỏ nhất.Phương pháp giải:
Với hai điểm $\displaystyle M$ và $\displaystyle N$ tìm được ở câu trên, tính độ dài đoạn thẳng $\displaystyle MN$ theo công thức: $\displaystyle MN = \sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2}} = \sqrt {f\left( x \right)} .$
+) Khảo sát và tìm giá trị nhỏ nhất của hàm số $\displaystyle y=f\left(x\right)$ từ đó suy ra độ dài nhỏ nhất của $\displaystyle MN.$
Lời giải chi tiết:
Gọi $\displaystyle M\left( {{x_M}; {y_M}} \right)$ và $\displaystyle N\left( {{x_N}; {y_N}} \right)$ là hai giao điểm của $\displaystyle \left(C\right)$ và đường tahnwgr $\displaystyle y=2x+m.$
Theo định lí Vi-et ta có: $\displaystyle \left\{ \matrix{{x_M} + {x_N} = - {{m + 1} \over 2} \hfill \cr {x_M}.{x_N} = {{m - 3} \over 2} \hfill \cr} \right.$
$\displaystyle \begin{array}{l}
M{N^2} = {\left( {{x_M} - {x_N}} \right)^2} + {\left( {{y_M} - {y_N}} \right)^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + {\left[ {2{x_M} + m - \left( {2{x_N} + m} \right)} \right]^2}\\
= {\left( {{x_M} - {x_N}} \right)^2} + 4{\left( {{x_M} - {x_N}} \right)^2}\\
= 5{\left( {{x_M} - {x_N}} \right)^2}\\
= 5\left[ {{{\left( {{x_M} + {x_N}} \right)}^2} - 4{x_M}{x_N}} \right]\\
= 5\left[ {{{\left( { - \dfrac{{m + 1}}{2}} \right)}^2} - 4.\dfrac{{m - 3}}{2}} \right]\\
= 5\left( {\dfrac{{{m^2} + 2m + 1}}{4} - 2m + 6} \right)\\
= 5.\dfrac{{{m^2} - 6m + 25}}{4} \\ = \dfrac{5}{4}\left[ {\left( {{m^2} - 6m + 9} \right) + 16} \right]\\
= \dfrac{5}{4}\left[ {{{\left( {m - 3} \right)}^2} + 16} \right].
\end{array}$
Ta có: $\displaystyle {\left( {m - 3} \right)^2} \ge 0 \forall m \Rightarrow {\left( {m - 3} \right)^2} + 16 \ge 16$
$\displaystyle \begin{array}{l}
\Rightarrow M{N^2} \ge \dfrac{5}{4}.16 = 20.\\
\Rightarrow MN \ge 2\sqrt 5 .
\end{array}$
Dấu "=" xảy ra $\displaystyle \Leftrightarrow m - 3 = 0 \Leftrightarrow m = 3.$
Vậy độ dài $\displaystyle MN$ nhỏ nhất bằng $\displaystyle 2\sqrt5$ khi $\displaystyle m=3.$
Câu d
d) Tiếp tuyến tại một điểm $\displaystyle S$ bất kì của $\displaystyle \left(C\right)$ luôn cắt hai tiệm cận của $\displaystyle \left(C\right)$ tại $\displaystyle P$ và $\displaystyle Q$. Chứng minh rằng $\displaystyle S$ là trung điểm của $\displaystyle PQ$.Phương pháp giải:
Gọi $\displaystyle S\left(x_0; y_0\right)$ là 1 điểm bất kì thuộc đồ thị hàm số $\displaystyle \left(C\right).$ Khi đó phương trình tiếp tuyến của đồ thị hàm số tại $\displaystyle S$ là: $\displaystyle \Delta: y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.$
+) Tìm các giao điểm $\displaystyle P, Q$ của tiếp tuyến $\displaystyle \Delta$ với các đường tiệm cận.
+) Khi đó $\displaystyle S$ là trung điểm của $\displaystyle PQ\Leftrightarrow \left\{ \begin{array}{l}{x_0} = \dfrac{{{x_P} + {x_Q}}}{2}\\{y_0} = \dfrac{{{y_P} + {y_Q}}}{2}\end{array} \right..$
Lời giải chi tiết:
Giả sử $\displaystyle S\left(x_0;y_0\right)$ là điểm bất kì thuộc (C)
Phương trình tiếp tuyến $\displaystyle Δ$ của (C) tại $\displaystyle S$ là:
$\displaystyle \eqalign{
& y - y_0 = y'\left({x_0}\right)\left(x - {x_0}\right) \cr
& \Leftrightarrow y = {{ - 2} \over {{{\left({x_0} + 1\right)}^2}}}\left(x - {x_0}\right) + {{{x_0} + 3} \over {{x_0} + 1}} \cr} $
Tiệm cận đứng: $\displaystyle x=-1$ và tiệm cận ngang: $\displaystyle y=1.$
Giả sử $\displaystyle Δ$ cắt tiệm cận ngang tại $\displaystyle P\left(x_P; 1\right)$. Khi đó:
$\displaystyle \begin{array}{l}
\dfrac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( {{x_P} - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} + 1}} = 1\\
\Leftrightarrow - 2{x_P} + 2{x_0} + x_0^2 + 4{x_0} + 3 = x_0^2 + 2{x_0} + 1\\
\Leftrightarrow - 2{x_P} = - 4{x_0} - 2\\
\Leftrightarrow {x_P} = 2{x_0} + 1\\
\Rightarrow P\left( {2{x_0} + 1; 1} \right).
\end{array}$
$\displaystyle Δ$ cắt tiệm cận đứng tại $\displaystyle Q\left( - 1; y_Q\right).$ Khi đó:
$\displaystyle \begin{array}{l}
\dfrac{{ - 2}}{{{{\left( {{x_0} + 1} \right)}^2}}}\left( { - 1 - {x_0}} \right) + \dfrac{{{x_0} + 3}}{{{x_0} + 1}} = {y_Q}\\
\Leftrightarrow 2 + 2{x_0} + x_0^2 + 4{x_0} + 3 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow x_0^2 + 6{x_0} + 5 = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow \left( {{x_0} + 1} \right)\left( {{x_0} + 5} \right) = {y_Q}{\left( {{x_0} + 1} \right)^2}\\
\Leftrightarrow {y_Q} = \dfrac{{{x_0} + 5}}{{{x_0} + 1}}.\\
\Rightarrow Q\left( { - 1; \dfrac{{{x_0} + 5}}{{{x_0} + 1}}} \right)
\end{array}$
$\displaystyle \Rightarrow \left\{ \begin{array}{l}
{x_P} + {x_Q} = 2{x_0} + 1 - 1 = 2{x_0} = 2{x_S}\\
{y_P} + {y_Q} = 1 + \dfrac{{{x_0} + 5}}{{{x_0} + 1}} = \dfrac{{2{x_0} + 6}}{{{x_0} + 1}} = \dfrac{{2\left( {{x_0} + 3} \right)}}{{{x_0} + 1}} = 2{y_0} = 2{y_S}.
\end{array} \right.$
Vậy $\displaystyle S$ là trung điểm của $\displaystyle PQ$.
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!