Câu hỏi:
$y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10$ ;
Phương pháp giải:
Quy tắc 1 tìm cực trị của hàm số:
Bước 1: Tìm tập xác định.
Bước 2: Tính $f'\left( x \right)$. Tìm các điểm mà tại đó $f'\left( x \right)$ bằng 0 hoặc $f'\left( x \right)$ không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Lời giải chi tiết:
Tập xác định: $D = \mathbb R$
$\eqalign{
& y' = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y' = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 2\Rightarrow {y = - 54} \hfill \cr
x = - 3 \Rightarrow {y = 71} \hfill \cr} \right. \cr} $
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( { - 3;2} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( {2; + \infty } \right)\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
Bảng biến thiên:
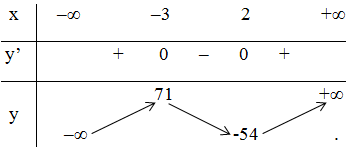
Hàm số đạt cực đại tại $x = -3$ và $y$ CĐ $= 71$
Hàm số đạt cực tiểu tại $x = 2$ và $y$ CT $= -54$
Lời giải chi tiết:
Tập xác định: $D =\mathbb R$
$y' = 4{{\rm{x}}^3} + 4{\rm{x}} = 4{\rm{x}}\left( {{x^2} + 1} \right)$ ;
$y' = 0 \Leftrightarrow x = 0\Rightarrow {y = - 3}$
$\begin{array}{l}y' > 0 \Rightarrow x > 0\\y' < 0 \Rightarrow x < 0\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = + \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
Bảng biến thiên:
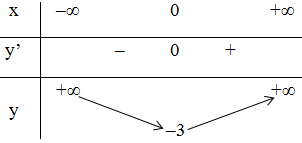
Hàm số đạt cực tiểu tại $x = 0$ và $y$ CT $= -3$
Lời giải chi tiết:
Tập xác định: $D = \mathbb R$ \ { 0 }
$\eqalign{
& y' = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};y' = 0 \cr
& \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \Rightarrow {y = 2} \hfill \cr
x = - 1 \Rightarrow {y = - 2} \hfill \cr} \right. \cr}$
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( { - 1;1} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
$\mathop {\lim }\limits_{x \Rightarrow {0^ - }} y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow {0^ + }} y = + \infty $
Bảng biến thiên
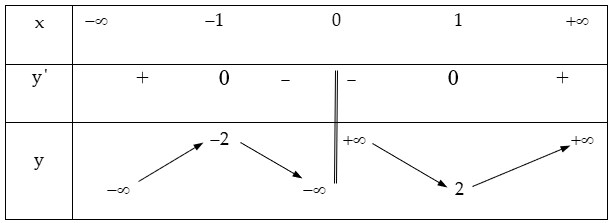
Hàm số đạt cực đại tại $x = -1$, $y$ CĐ $= -2$
Hàm số đạt cực tiểu tại $x = 1$, $y$ CT $= 2$
Lời giải chi tiết:
Tập xác định $D = \mathbb R$
$\begin{array}{l}
y' = \left( {{x^3}} \right)'{\left( {1 - x} \right)^2} + {x^3}\left[ {{{\left( {1 - x} \right)}^2}} \right]'\\
= 3{x^2}{\left( {1 - x} \right)^2} + {x^3}.2\left( {1 - x} \right)\left( {1 - x} \right)'\\
= 3{x^2}{\left( {1 - x} \right)^2} + 2{x^3}\left( {1 - x} \right)\left( { - 1} \right)\\
= 3{x^2}{\left( {1 - x} \right)^2} - 2{x^3}\left( {1 - x} \right)\\
= {x^2}\left( {1 - x} \right)\left[ {3\left( {1 - x} \right) - 2x} \right]\\
= {x^2}\left( {1 - x} \right)\left( {3 - 3x - 2x} \right)\\
= {x^2}\left( {1 - x} \right)\left( {3 - 5x} \right)
\end{array}$
$\eqalign{
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 1\Rightarrow {y = 0} \hfill \cr
x = {3 \over 5}\Rightarrow {y = {{108} \over {3125}}} \hfill \cr
x = 0 \Rightarrow {y = 0}\hfill \cr} \right. \cr} $
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( {\dfrac{3}{5};1} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ;\dfrac{3}{5}} \right) \cup \left( {1; + \infty } \right)\\\mathop {\lim }\limits_{x \Rightarrow -\infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty \end{array}$
Bảng biến thiên:
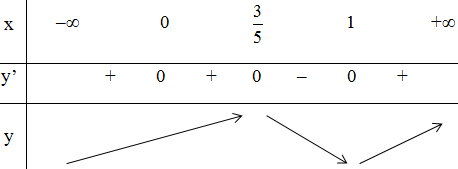
Hàm số đạt cực đại tại $x = {3 \over 5};y = {{108} \over {3125}}$
Hàm số đạt cực tiểu tại $x = 1$, $y$ CT = $ 0$
Lời giải chi tiết:
Vì $x^2$ – $ x + 1 > 0, ∀ ∈ \mathbb R$ nên tập xác định : $D = \mathbb R$
$y' = {{2{\rm{x}} - 1} \over {2\sqrt {{x^2} - x + 1} }};y' = 0 \Leftrightarrow x = {1 \over 2}\Rightarrow {y = {{\sqrt 3 } \over 2}}$
$\begin{array}{l}y' > 0 \Leftrightarrow x > \dfrac{1}{2}; y' < 0 \Leftrightarrow x < \dfrac{1}{2}\\
\mathop {\lim }\limits_{x \Rightarrow - \infty } y = + \infty , \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty \end{array}$
Bảng biến thiên:
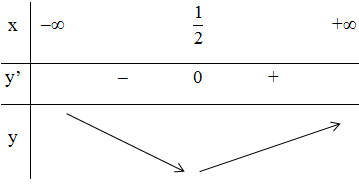
Hàm số đạt cực tiểu tại $x = {1 \over 2};{y_{CT}} = {{\sqrt 3 } \over 2}$
Câu a
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :$y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10$ ;
Phương pháp giải:
Quy tắc 1 tìm cực trị của hàm số:
Bước 1: Tìm tập xác định.
Bước 2: Tính $f'\left( x \right)$. Tìm các điểm mà tại đó $f'\left( x \right)$ bằng 0 hoặc $f'\left( x \right)$ không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Lời giải chi tiết:
Tập xác định: $D = \mathbb R$
$\eqalign{
& y' = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y' = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = 2\Rightarrow {y = - 54} \hfill \cr
x = - 3 \Rightarrow {y = 71} \hfill \cr} \right. \cr} $
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( { - 3;2} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( {2; + \infty } \right)\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
Bảng biến thiên:

Hàm số đạt cực đại tại $x = -3$ và $y$ CĐ $= 71$
Hàm số đạt cực tiểu tại $x = 2$ và $y$ CT $= -54$
Câu b
$y{\rm{ }} = {\rm{ }}x{^4} + {\rm{ }}2{x^2}-{\rm{ }}3$ ;Lời giải chi tiết:
Tập xác định: $D =\mathbb R$
$y' = 4{{\rm{x}}^3} + 4{\rm{x}} = 4{\rm{x}}\left( {{x^2} + 1} \right)$ ;
$y' = 0 \Leftrightarrow x = 0\Rightarrow {y = - 3}$
$\begin{array}{l}y' > 0 \Rightarrow x > 0\\y' < 0 \Rightarrow x < 0\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = + \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
Bảng biến thiên:

Hàm số đạt cực tiểu tại $x = 0$ và $y$ CT $= -3$
Câu c
$y = x + {1 \over x}$Lời giải chi tiết:
Tập xác định: $D = \mathbb R$ \ { 0 }
$\eqalign{
& y' = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};y' = 0 \cr
& \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \Rightarrow {y = 2} \hfill \cr
x = - 1 \Rightarrow {y = - 2} \hfill \cr} \right. \cr}$
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( { - 1;1} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\end{array}$
$\mathop {\lim }\limits_{x \Rightarrow - \infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty $
$\mathop {\lim }\limits_{x \Rightarrow {0^ - }} y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow {0^ + }} y = + \infty $
Bảng biến thiên

Hàm số đạt cực đại tại $x = -1$, $y$ CĐ $= -2$
Hàm số đạt cực tiểu tại $x = 1$, $y$ CT $= 2$
Câu d
$y{\rm{ }} = {\rm{ }}{x^3}{\left( {1{\rm{ }}-{\rm{ }}x} \right)^{2}}$ ;Lời giải chi tiết:
Tập xác định $D = \mathbb R$
$\begin{array}{l}
y' = \left( {{x^3}} \right)'{\left( {1 - x} \right)^2} + {x^3}\left[ {{{\left( {1 - x} \right)}^2}} \right]'\\
= 3{x^2}{\left( {1 - x} \right)^2} + {x^3}.2\left( {1 - x} \right)\left( {1 - x} \right)'\\
= 3{x^2}{\left( {1 - x} \right)^2} + 2{x^3}\left( {1 - x} \right)\left( { - 1} \right)\\
= 3{x^2}{\left( {1 - x} \right)^2} - 2{x^3}\left( {1 - x} \right)\\
= {x^2}\left( {1 - x} \right)\left[ {3\left( {1 - x} \right) - 2x} \right]\\
= {x^2}\left( {1 - x} \right)\left( {3 - 3x - 2x} \right)\\
= {x^2}\left( {1 - x} \right)\left( {3 - 5x} \right)
\end{array}$
$\eqalign{
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 1\Rightarrow {y = 0} \hfill \cr
x = {3 \over 5}\Rightarrow {y = {{108} \over {3125}}} \hfill \cr
x = 0 \Rightarrow {y = 0}\hfill \cr} \right. \cr} $
$\begin{array}{l}y' < 0 \Leftrightarrow x \in \left( {\dfrac{3}{5};1} \right)\\y' > 0 \Leftrightarrow x \in \left( { - \infty ;\dfrac{3}{5}} \right) \cup \left( {1; + \infty } \right)\\\mathop {\lim }\limits_{x \Rightarrow -\infty } y = - \infty ; \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty \end{array}$
Bảng biến thiên:

Hàm số đạt cực đại tại $x = {3 \over 5};y = {{108} \over {3125}}$
Hàm số đạt cực tiểu tại $x = 1$, $y$ CT = $ 0$
Câu e
$y = \sqrt {{x^2} - x + 1}$Lời giải chi tiết:
Vì $x^2$ – $ x + 1 > 0, ∀ ∈ \mathbb R$ nên tập xác định : $D = \mathbb R$
$y' = {{2{\rm{x}} - 1} \over {2\sqrt {{x^2} - x + 1} }};y' = 0 \Leftrightarrow x = {1 \over 2}\Rightarrow {y = {{\sqrt 3 } \over 2}}$
$\begin{array}{l}y' > 0 \Leftrightarrow x > \dfrac{1}{2}; y' < 0 \Leftrightarrow x < \dfrac{1}{2}\\
\mathop {\lim }\limits_{x \Rightarrow - \infty } y = + \infty , \mathop {\lim }\limits_{x \Rightarrow + \infty } y = + \infty \end{array}$
Bảng biến thiên:

Hàm số đạt cực tiểu tại $x = {1 \over 2};{y_{CT}} = {{\sqrt 3 } \over 2}$
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!