Câu hỏi: Cho hàm số: \(f(x) = ax^2– 2(a + 1)x + a + 2 (a ≠ 0)\)
Phương pháp giải:
Nhẩm nghiệm, đưa phương trình \(f(x)=0\) về dạng phương trình tích để tìm nghiệm của phương trình.
Lời giải chi tiết:
Ta có:
\(f\left( x \right) = 0\) \(\Leftrightarrow a{x^2} - 2(a + 1)x + a + 2 = 0\)
Phương trình trên có \(A = a; B = - 2\left( {a + 1} \right), C = a + 2\) và
\(A + B + C\) \(= a - 2\left( {a + 1} \right) + a + 2\) \(= a - 2a - 2 + a + 2 = 0\)
Do đó phương trình có hai nghiệm phân biệt \({x_1} = 1,{x_2} = \dfrac{C}{A} = \dfrac{{a + 2}}{a}\).
Phương pháp giải:
+) Dựa vào hệ thức Vi-ét để tính tổng và tích các nghiệm của phương trình \(f(x)=0.\)
+) Khảo sát sự biến thiên của đồ thị hàm số và vẽ đồ thị hàm số qua các bước đã được học.
Lời giải chi tiết:
* Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
\(\displaystyle S = {{2a + 2} \over a}, P = {{a + 2} \over a}\)
* Khảo sát sự biến thiên và vẽ đồ thị hàm số \(\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}\)
- Tập xác định : \((-∞; 0) ∪ (0, +∞)\)
- Sự biến thiên: \(\displaystyle S' = - {2 \over {{a^2}}} < 0,\forall a \in ( - \infty; 0) \cup (0; + \infty)\) nên hàm số nghịch biến trên hai khoảng \((-∞; 0)\) và \((0; +∞)\)
- Cực trị: Hàm số không có cực trị.
- Giới hạn tại vô cực và tiệm cận ngang.
\(\eqalign{
& \mathop {\lim }\limits_{a \to + \infty } S = \mathop {\lim }\limits_{a \to + \infty } (2 + {2 \over a}) = 2 \cr
& \mathop {\lim }\limits_{a \to - \infty } S = \mathop {\lim }\limits_{a \to - \infty } (2 + {2 \over a}) = 2 \cr} \)
Vậy \(S = 2\) là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
\(\eqalign{
& \mathop {\lim }\limits_{a \to {0^ + }} S = \mathop {\lim }\limits_{a \to {0^ + }} (2 + {2 \over a}) = + \infty \cr
& \mathop {\lim }\limits_{a \to {0^ - }} S = \mathop {\lim }\limits_{a \to {0^ - }} (2 + {2 \over a}) = - \infty \cr} \)
Vậy \(a = 0\) là tiệm cận đứng.
- Bảng biến thiên:
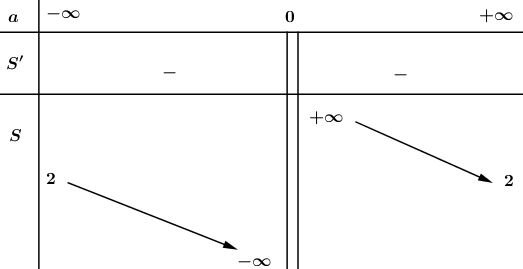
Đồ thị hàm số:
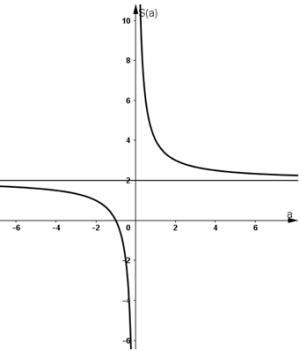
Đồ thị không cắt trục tung, cắt trục hoành tại \(a = -1\)
* Khảo sát sự biến thiên và vẽ đồ thị hàm số \(\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}\)
Tập xác định: \(D = \mathbb R\backslash {\rm{\{ }}0\} \)
\(\displaystyle P' = {{ - 2} \over {{a^2}}} < 0,\forall a \in D\)
\(\mathop {\lim }\limits_{a \to {0^ - }} S = - \infty ⇒ \) Tiệm cận đứng: \(a = 0\)
\(\mathop {\lim }\limits_{a \to \pm \infty } S = 1⇒\) Tiệm cận ngang: \(P = 1\)
Đồ thị hàm số:
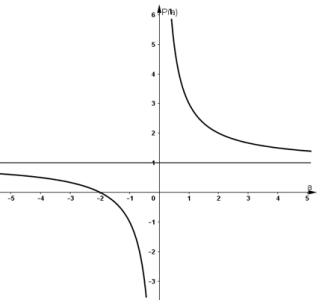
Ngoài ra: đồ thị hàm số \(\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}\) có thể nhận được bằng cách tịnh tiến đồ thị \(\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}\) dọc theo trục tung xuống phía dưới \(1\) đơn vị.
Câu a
a) Chứng tỏ rằng phương trình \(f(x) = 0\) luôn có nghiệm thực. Tính các nghiệm đó.Phương pháp giải:
Nhẩm nghiệm, đưa phương trình \(f(x)=0\) về dạng phương trình tích để tìm nghiệm của phương trình.
Lời giải chi tiết:
Ta có:
\(f\left( x \right) = 0\) \(\Leftrightarrow a{x^2} - 2(a + 1)x + a + 2 = 0\)
Phương trình trên có \(A = a; B = - 2\left( {a + 1} \right), C = a + 2\) và
\(A + B + C\) \(= a - 2\left( {a + 1} \right) + a + 2\) \(= a - 2a - 2 + a + 2 = 0\)
Do đó phương trình có hai nghiệm phân biệt \({x_1} = 1,{x_2} = \dfrac{C}{A} = \dfrac{{a + 2}}{a}\).
Câu b
b) Tính tổng \(S\) và tích \(P\) của các nghiệm của phương trình \(f(x) = 0\). Khảo sát sự biến thiên và vẽ đồ thị hàm số của \(S\) và \(P\) theo \(a\).Phương pháp giải:
+) Dựa vào hệ thức Vi-ét để tính tổng và tích các nghiệm của phương trình \(f(x)=0.\)
+) Khảo sát sự biến thiên của đồ thị hàm số và vẽ đồ thị hàm số qua các bước đã được học.
Lời giải chi tiết:
* Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
\(\displaystyle S = {{2a + 2} \over a}, P = {{a + 2} \over a}\)
* Khảo sát sự biến thiên và vẽ đồ thị hàm số \(\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}\)
- Tập xác định : \((-∞; 0) ∪ (0, +∞)\)
- Sự biến thiên: \(\displaystyle S' = - {2 \over {{a^2}}} < 0,\forall a \in ( - \infty; 0) \cup (0; + \infty)\) nên hàm số nghịch biến trên hai khoảng \((-∞; 0)\) và \((0; +∞)\)
- Cực trị: Hàm số không có cực trị.
- Giới hạn tại vô cực và tiệm cận ngang.
\(\eqalign{
& \mathop {\lim }\limits_{a \to + \infty } S = \mathop {\lim }\limits_{a \to + \infty } (2 + {2 \over a}) = 2 \cr
& \mathop {\lim }\limits_{a \to - \infty } S = \mathop {\lim }\limits_{a \to - \infty } (2 + {2 \over a}) = 2 \cr} \)
Vậy \(S = 2\) là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
\(\eqalign{
& \mathop {\lim }\limits_{a \to {0^ + }} S = \mathop {\lim }\limits_{a \to {0^ + }} (2 + {2 \over a}) = + \infty \cr
& \mathop {\lim }\limits_{a \to {0^ - }} S = \mathop {\lim }\limits_{a \to {0^ - }} (2 + {2 \over a}) = - \infty \cr} \)
Vậy \(a = 0\) là tiệm cận đứng.
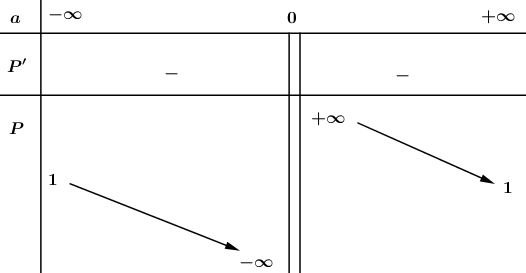
- Bảng biến thiên:

Đồ thị hàm số:

Đồ thị không cắt trục tung, cắt trục hoành tại \(a = -1\)
* Khảo sát sự biến thiên và vẽ đồ thị hàm số \(\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}\)
Tập xác định: \(D = \mathbb R\backslash {\rm{\{ }}0\} \)
\(\displaystyle P' = {{ - 2} \over {{a^2}}} < 0,\forall a \in D\)
\(\mathop {\lim }\limits_{a \to {0^ - }} S = - \infty ⇒ \) Tiệm cận đứng: \(a = 0\)
\(\mathop {\lim }\limits_{a \to \pm \infty } S = 1⇒\) Tiệm cận ngang: \(P = 1\)

Đồ thị hàm số:

Ngoài ra: đồ thị hàm số \(\displaystyle P = {{a + 2} \over a} = 1 + {2 \over a}\) có thể nhận được bằng cách tịnh tiến đồ thị \(\displaystyle S = {{2a + 2} \over a} = 2 + {2 \over a}\) dọc theo trục tung xuống phía dưới \(1\) đơn vị.
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!