Tỉ số P/Po gần nhất giá trị nào sau đây

giolanh

giolanh

Active Member
Bài toán
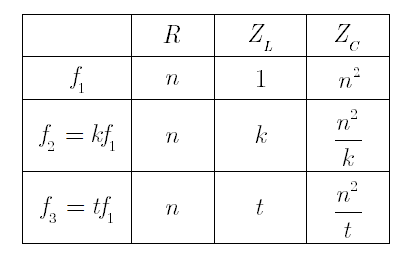
Cho mạch điện xoay chiều $RLC$ mắc nối tiếp, cuộn dây thuần cảm. Biết $L=CR^{2}$. Đặt vào 2 đầu đoạn mạch điện áp xoay chiều ổn định, mạch tiêu thụ cùng công suất $P_o$ với 2 giá trị $f_1$ và $f_2$. Khi tần số $f_3$ thì điện áp hiệu dụng trên tụ cực đại và lúc này mạch tiêu thụ cũng công suất $P$. Nếu $f_1+f_2=\sqrt{12}f_3$ thì tỉ số $\dfrac{P}{P_o}$ gần giá trị nào nhất
A. 0,85
B. 052
C. 1,15
D. 2.2
Thấy câu của bạn nào vừa đăng nhưng xóa rồi hay nên mình đăng lại cho mọi người cùng xem và cách giải của mình hơi dài ai có cách hay và nhanh hơn không, chứ mấy phút bài này hơi vất
 
Sort by date Sort by votes
Mục đích của mình là dùng công thức $P=\dfrac{U^{2}}{R}.\cos ^{2}\varphi $
*$f_3$ Thay đổi $f$ để $U_c$ max thì
$\left(\omega \right)^{2}=\dfrac{2LC-R^{2}C^{2}}{2L^{2}C^{2}}$
biến đổi với $\dfrac{L}{C}=R^{2}$ có $\omega _3=\dfrac{R}{\sqrt{2}L}$
$\Leftrightarrow Z_L=\dfrac{R}{\sqrt{2}}$
rồi sau đó tìm mối liên hệ giữa 3 giá trị $Z_L, R, Z_c$ ra được $\cos ^{2}\omega _3=\dfrac{2}{3}$

*$f_1, f_2$
giờ tìm mối liên hệ $f_1$ và $f_3$ ; $f_2$ và $f_3$ từ đó giải và ta áp dụng công thức
$\cos \varphi _1=\cos \varphi _2=\dfrac{1}{\sqrt{1+k\left(\sqrt{\dfrac{\omega _1}{\omega _2}}-\sqrt{\dfrac{\omega _2}{\omega _1}}\right)^{2}}}$
với $\dfrac{L}{C}=kR^{2}$
$\omega _o^{2}=\omega _1 \omega _2=\dfrac{1}{LC}=\omega _3\omega _4$ với $\omega _4 $là thay đổi f để $U_L$ max
rút ra được $\dfrac{\omega _3}{\omega _4}=\dfrac{1}{2}$
$\Rightarrow \omega _1.\omega _2=2.\left(\omega _3\right)^{2}$
Giải hệ có
$\omega _1=\left(1+\sqrt{3}\right)f_3$
$\omega _1=\left(-1+\sqrt{3}\right)f_3$
thay vào công thức trên có
$\left(\cos \varphi _1\right)^{2}=\dfrac{1}{3}$
$\Rightarrow\dfrac{P}{P_o}=2$
 
Upvote 0 Downvote
Gợi ý :Bài này sử dụng 2 dữ kiện;
$f_{1}.f_{2}=f_{3}^{2}$ và
$\cos \varphi =\dfrac{1}{\sqrt{1+\dfrac{L}{R^{2}C}\left(\dfrac{f_{1}}{f_{2}}+\dfrac{f_{2}}{f_{1}}-2}\right)}$
Đi tính tỉ lệ $f_{1}$ và $f_{2} rồi tính là xong.
 
Last edited:
Upvote 0 Downvote
hoankuty đã viết:
Gợi ý :Bài này sử dụng 2 dữ kiện;
  • $f_{1}.f_{2}=f_{3}^{2}$
  • $\cos \varphi =\dfrac{\cos \varphi _{max}}{\sqrt{1+\dfrac{L}{CR^{2}}\left(\sqrt{\dfrac{f_{1}}{f_{2}}}-\sqrt{\dfrac{f_{2}}{f_{1}}}}\right)^{2}}$
Đi tính tỉ lệ $f_{1}$ và $f_{2} rồi tính là xong.
Click để xem thêm...
? Sao lại bằng $f_{1}.f_{2}=f_{3}^{2}$ thôi ạ
 
Upvote 0 Downvote
Vậy đi theo hướng này. Chỉ thêm có 1 vài bước thôi :
Ban đầu : $\dfrac{fc}{f_{L}}=1-\dfrac{L}{2R^{2}C}\rightarrow f_{L}=2f_{C}$
Khi đó tính được : $\cos \varphi _{C}=\dfrac{\sqrt{6}}{3}$
Mà $f_{L}.f_{C}=f_{o}^{2}$
$\rightarrow f_{o}=\sqrt{2}f_{C}\rightarrow f_{1}+f_{2}=\sqrt{6}f_{o}$
Kết hợp $f_{1}.f_{2}=f_{o}^{2}$
Tiếp : với $a=\dfrac{f_{1}}{f_{2}}$ thì :
$\cos \varphi _{1}^{2}=\dfrac{1}{1+\dfrac{L}{R^{2}C}\left(a+\dfrac{1}{a}-2\right)}$
Tính a rồi làm tiếp.
 
Upvote 0 Downvote
Lời giải

Từ giả thiết ta có: ${Z_L}.{Z_C} = {R^2},\forall \omega > 0.$
Khi đó ta có bảng chuẩn hóa sau:
anh.png

Khi đó, kết hợp giả thiết ta có:
\[\left\{ \begin{array}{l}
{\left({{n^2} - 1} \right)^2} = {\left({\dfrac{{{n^2}}}{k} - k} \right)^2}\\
n = t\sqrt 2 \\
k = \sqrt {12} t - 1
\end{array} \right.\iff \left\{ \begin{array}{l}
k = 2 + \sqrt 3 \\
n = \dfrac{{3 + \sqrt 3 }}{6}\\
t = \dfrac{{\sqrt 3 + 1}}{2}
\end{array} \right..\]
Giải hệ trên chỉ cần thay ẩn $k$.
Và ta suy ra:
\[\dfrac{P}{{{P_o}}} = {\left({\dfrac{{\cos \varphi }}{{\cos {\varphi _o}}}} \right)^2} = \dfrac{{\dfrac{2}{3}}}{{\dfrac{1}{3}}} = 2.\]
 
Upvote 0 Downvote
Nguyễn Đình Huynh đã viết:
Lời giải

Từ giả thiết ta có: ${Z_L}.{Z_C} = {R^2},\forall \omega > 0.$
Khi đó ta có bảng chuẩn hóa sau:
anh.png
Khi đó, kết hợp giả thiết ta có:
\[\left\{ \begin{array}{l}
{\left({{n^2} - 1} \right)^2} = {\left({\dfrac{{{n^2}}}{k} - k} \right)^2}\\
n = t\sqrt 2 \\
k = \sqrt {12} t - 1
\end{array} \right.\iff \left\{ \begin{array}{l}
k = 2 + \sqrt 3 \\
n = \dfrac{{3 + \sqrt 3 }}{6}\\
t = \dfrac{{\sqrt 3 + 1}}{2}
\end{array} \right..\]
Giải hệ trên chỉ cần thay ẩn $k$.
Và ta suy ra:
\[\dfrac{P}{{{P_o}}} = {\left({\dfrac{{\cos \varphi }}{{\cos {\varphi _o}}}} \right)^2} = \dfrac{{\dfrac{2}{3}}}{{\dfrac{1}{3}}} = 2.\]
Click để xem thêm...
Một hướng đi cho những ai "ngại" dùng công thức. Khá tự nhiên, nhưng cũng phải nói rằng người làm phải có những kĩ năng toán học cũng như 1 tâm lý đủ để làm tới đáp án.
 
Upvote 0 Downvote
hoankuty đã viết:
Một hướng đi cho những ai "ngại" dùng công thức. Khá tự nhiên, nhưng cũng phải nói rằng người làm phải có những kĩ năng toán học cũng như 1 tâm lý đủ để làm tới đáp án.
Click để xem thêm...
Là mọi người sợ phương trình bậc 5 kí. Nhưng để ý với ẩn $k \ne \pm 1$ sẽ luôn loại được trước hai nghiệm, phương trình bậc ba còn lại cứ thế mà bấm máy tính :))
 
Upvote 0 Downvote
Nguyễn Đình Huynh đã viết:
Lời giải

Từ giả thiết ta có: ${Z_L}.{Z_C} = {R^2},\forall \omega > 0.$
Khi đó ta có bảng chuẩn hóa sau:
anh.png
Khi đó, kết hợp giả thiết ta có:
\[\left\{ \begin{array}{l}
{\left({{n^2} - 1} \right)^2} = {\left({\dfrac{{{n^2}}}{k} - k} \right)^2}\\
n = t\sqrt 2 \\
k = \sqrt {12} t - 1
\end{array} \right.\iff \left\{ \begin{array}{l}
k = 2 + \sqrt 3 \\
n = \dfrac{{3 + \sqrt 3 }}{6}\\
t = \dfrac{{\sqrt 3 + 1}}{2}
\end{array} \right..\]
Giải hệ trên chỉ cần thay ẩn $k$.
Và ta suy ra:
\[\dfrac{P}{{{P_o}}} = {\left({\dfrac{{\cos \varphi }}{{\cos {\varphi _o}}}} \right)^2} = \dfrac{{\dfrac{2}{3}}}{{\dfrac{1}{3}}} = 2.\]
Click để xem thêm...
Bái phục ạ :v
Nhưng cái ra hệ #huynh trình bày rõ ràng ra nữa cho mn hiểu ạ
 
Upvote 0 Downvote
Bạn phải đăng nhập hoặc đăng kí để trả lời.

Các chủ đề tương tự

T
  • Article
Đặt điện áp xoay chiều có giá trị hiệu dụng không đối và tần số...
Trả lời
0
Đọc
116
The Funny
T
T
  • Article
Đặt điện áp xoay chiều có giá trị hiệu dụng không đồi và tần số...
Trả lời
0
Đọc
234
The Funny
T
T
  • Article
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đối...
Trả lời
0
Đọc
152
The Funny
T
T
  • Article
Đặt điện áp xoay chiều có giá trị hiệu dụng $U$ vào hai đầu đoạn...
Trả lời
0
Đọc
213
The Funny
T
T
  • Article
Đặt điện áp xoay chiều có giá trị hiệu dụng $U$ vào hai đầu một...
Trả lời
0
Đọc
147
The Funny
T

Quảng cáo

Back
Top