You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Zix.vn - Học online chất lượng cao
Tài liệu mới
Đề thi chọn học sinh giỏi môn Toán 9 năm học 2022 - 2023 - Tỉnh Hải Dương (giải chi tiết)
Đề thi chọn học sinh giỏi môn Toán 9 năm học 2022 - 2023 - Thành phố Hà Nội (giải chi tiết)
Đề thi học kỳ 1 môn Toán lớp 9 năm học 2022 - 2023 - Phòng GD&ĐT Thạch Thất - Hà Nội (có đáp án)
Đề thi học kỳ 1 môn Toán lớp 9 năm học 2022 - 2023 - Phòng GD&ĐT TP Ninh Bình (có đáp án)
Tin tức
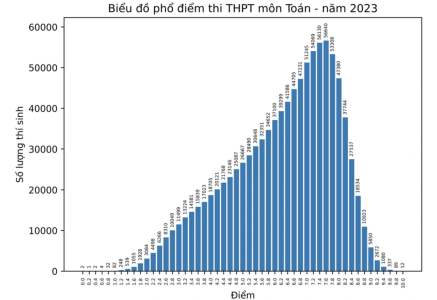
Sáng 18/7, Bộ Giáo dục và Đào tạo công bố phổ điểm các môn thi tốt nghiệp THPT năm 2023. Cụ thể phổ điểm các môn thi tốt nghiệp THPT 2023 như sau:
Môn Toán
Tổng số thí sinh
1,003,372
Điểm trung bình
6.25
Trung vị
6.6
Số thí sinh đạt điểm <=1
123
0.012 %
Số thí sinh đạt điểm dưới...
Đề thi tốt nghiệp THPT môn Tiếng Anh có cấu trúc quen thuộc, nhưng nhiều câu hỏi khó rõ nét so với năm ngoái. Nếu nắm chắc kiến thức, thí sinh dễ lấy điểm 6, 7.
Chiều 29/6, hơn một triệu thí sinh đã hoàn thành kỳ thi tốt nghiệp THPT với môn thi cuối là Ngoại ngữ (phần lớn thi Tiếng Anh) với...
Các năm trước Bộ GD&ĐT chỉ quy định một ngày công bố điểm thi tốt nghiệp THPT trên toàn quốc mà không giới hạn thời gian. Điều này đồng nghĩa với việc học sinh, phụ huynh và giáo viên phải thức khuya để xem điểm.
Tuy nhiên trong năm nay, Bộ GD&ĐT đã quy định cụ thể rằng điểm thi tốt nghiệp...
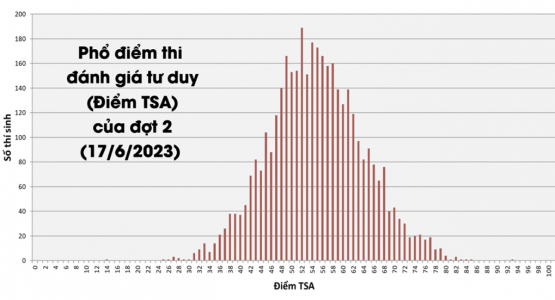
Kỳ thi đánh giá tư duy đợt hai của Đại học Bách khoa Hà Nội đã công bố kết quả với hơn 4.300 thí sinh tham gia. Điểm trung bình của đợt này là 54,32, cao hơn so với điểm trung bình 53,94 của đợt thi đầu tiên với hơn 7.300 thí sinh.
Thí sinh đạt điểm cao nhất trong đợt thi này là 92,83/100, và...
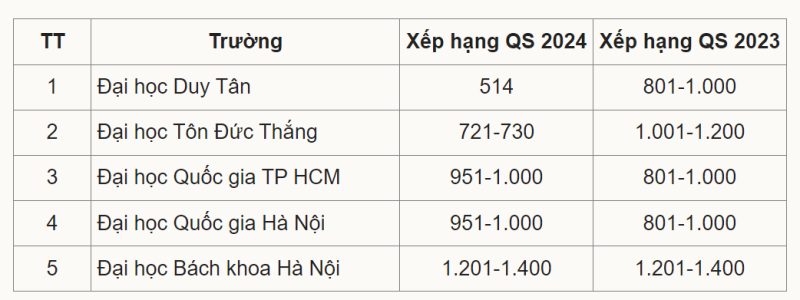
Bốn trường đại học của Việt Nam đã vươn lên trong danh sách top 1.000 đại học hàng đầu trên toàn cầu, đây là thành tích đáng chú ý chưa từng có. Quacquarelli Symonds (QS), một tổ chức uy tín về xếp hạng giáo dục, đã công bố bảng xếp hạng đại học năm 2024 vào ngày 28/6 vừa qua. Việt Nam có tới 5...
Diễn đàn Zix.vn xin gửi lời chúc tốt đẹp nhất đến tất cả các bạn học sinh đang chuẩn bị bước vào kỳ thi quan trọng của cuộc đời - kỳ thi tốt nghiệp THPT. Đây là một chặng đường đầy khó khăn và thử thách, nhưng cũng là cơ hội để các bạn thể hiện tài năng và kiến thức mà đã tích lũy suốt thời gian...